english102
New member
- Joined
- Jul 8, 2018
- Messages
- 1
Good afternoon,
I am working on a math problem that i need some help with. I am just stuck on it and can not figure it out. I have worked on this problem multiple times, but i keep getting it wrong. Any help will be great. Thank you.
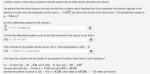
A body of mass 4 kg is projected vertically upward with an initial velocity 31 meters per second.
We assume that the forces acting on the body are the force of gravity and a retarding force of air resistance with direction opposite to the direction of motion and with magnitude [FONT=MathJax_Math-italic]c[FONT=MathJax_Main]|[/FONT][FONT=MathJax_Math-italic]v[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Math-italic]t[/FONT][FONT=MathJax_Main])[/FONT][FONT=MathJax_Main]|[/FONT][/FONT] where [FONT=MathJax_Math-italic]c[FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]0.45[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Math-italic]g[/FONT][FONT=MathJax_Math-italic]s[/FONT]c[/FONT] and [FONT=MathJax_Math-italic]v[FONT=MathJax_Main]([/FONT][FONT=MathJax_Math-italic]t[/FONT][FONT=MathJax_Main])[/FONT][/FONT] is the velocity of the ball at time t. The gravitational constant is [FONT=MathJax_Math-italic]g[FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]9.8[/FONT][FONT=MathJax_Math-italic]m[/FONT][FONT=MathJax_Main]/[/FONT][FONT=MathJax_Math-italic]s[/FONT][FONT=MathJax_Main]2[/FONT]g
a) Find a differential equation for the velocity
v:
dv/dt=???
[/FONT]
b) Solve the differential equation in part a) and find a formula for the velocity at any time [FONT=MathJax_Math-italic]tt[/FONT]:
v(t)=????
C) Find a formula for the position function at any time
t, if the initial position is s(0)=0:
s(t)=????
I am working on a math problem that i need some help with. I am just stuck on it and can not figure it out. I have worked on this problem multiple times, but i keep getting it wrong. Any help will be great. Thank you.
A body of mass 4 kg is projected vertically upward with an initial velocity 31 meters per second.
We assume that the forces acting on the body are the force of gravity and a retarding force of air resistance with direction opposite to the direction of motion and with magnitude [FONT=MathJax_Math-italic]c[FONT=MathJax_Main]|[/FONT][FONT=MathJax_Math-italic]v[/FONT][FONT=MathJax_Main]([/FONT][FONT=MathJax_Math-italic]t[/FONT][FONT=MathJax_Main])[/FONT][FONT=MathJax_Main]|[/FONT][/FONT] where [FONT=MathJax_Math-italic]c[FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]0.45[/FONT][FONT=MathJax_Math-italic]k[/FONT][FONT=MathJax_Math-italic]g[/FONT][FONT=MathJax_Math-italic]s[/FONT]c[/FONT] and [FONT=MathJax_Math-italic]v[FONT=MathJax_Main]([/FONT][FONT=MathJax_Math-italic]t[/FONT][FONT=MathJax_Main])[/FONT][/FONT] is the velocity of the ball at time t. The gravitational constant is [FONT=MathJax_Math-italic]g[FONT=MathJax_Main]=[/FONT][FONT=MathJax_Main]9.8[/FONT][FONT=MathJax_Math-italic]m[/FONT][FONT=MathJax_Main]/[/FONT][FONT=MathJax_Math-italic]s[/FONT][FONT=MathJax_Main]2[/FONT]g
a) Find a differential equation for the velocity
v:
dv/dt=???
[/FONT]
b) Solve the differential equation in part a) and find a formula for the velocity at any time [FONT=MathJax_Math-italic]tt[/FONT]:
v(t)=????
C) Find a formula for the position function at any time
t, if the initial position is s(0)=0:
s(t)=????