Solve sin(2θ) = 1

[Indranil]

If sin(2θ) = 1, then how to calculate the value of θ using 'the pi/4 + pi k' formula?

 

[Deleted member 4993]

If sin(2θ) = 1, then how to calculate the value of θ using 'the pi/4 + pi k' formula?

Hint:

sin(pi/2) = 1

 

[Dr.Peterson]

If sin 2 θ = 1, then how to calculate the value of θ using 'the pi/4 + pi k' formula?

The solution to the other problem we have been discussing is entirely irrelevant to this one. It is not a general formula that applies to any problem. Is there some reason you think it is related?

What you need to do here is to use your knowledge of the sine function to decide what angle(s) have their sine equal to 1. That will tell you what 2θ has to be. Then just divide each of the angles you found by 2 to get θ.

Please make some attempt, using some method you have been taught, so we have a starting point for discussing this. If you have a textbook, read its examples for equations like this, and do the same thing. If you have no textbook, find one and read it.

Also, once again, the problem is not complete as stated. You say "value" (singular), suggesting that you were asked only for one solution, which requires some restriction of the problem (for example, θ might have to be an acute angle). If it asks for all solutions, then you will need a solution that involves k. Please state the problem exactly as given to you, including instructions.

 

[Indranil]

The solution to the other problem we have been discussing is entirely irrelevant to this one. It is not a general formula that applies to any problem. Is there some reason you think it is related?

What you need to do here is to use your knowledge of the sine function to decide what angle(s) have their sine equal to 1. That will tell you what 2θ has to be. Then just divide each of the angles you found by 2 to get θ.

Please make some attempt, using some method you have been taught, so we have a starting point for discussing this. If you have a textbook, read its examples for equations like this, and do the same thing. If you have no textbook, find one and read it.

Also, once again, the problem is not complete as stated. You say "value" (singular), suggesting that you were asked only for one solution, which requires some restriction of the problem (for example, θ might have to be an acute angle). If it asks for all solutions, then you will need a solution that involves k. Please state the problem exactly as given to you, including instructions.

I have done below in two ways. please check my calculations below:
1. sin2θ = 1, (2) sinθ = sin 90,(2) sin θ/sin = sin 90 sin, 2θ/2 = 90/2, so θ = 45 degree
2. sinθ = 1, sin (90) = 1, so we get θ = 90, but here sin 2θ = 1, 2θ = 90, so θ = 45 degree

 

[mmm4444bot]

… please check my calculations …

sin2θ = 1

(2) sinθ = sin 90 …

Do not move the 2 like that because sin(2θ) and 2sin(θ) are not always equal.

For example, when θ=45° the equation sin(2θ)=2sin(θ) becomes 1=√2 which is false.

… (2) sin θ/sin = sin 90 sin …

Do not divide or multiply by sin because it's not a number. (It's a name.)

sinθ = 1, sin (90) = 1, so we get θ = 90, but here sin 2θ = 1, 2θ = 90, so θ = 45 degree

This way looks good. :smile:

 

[Indranil]

Do not move the 2 like that because sin(2θ) and 2sin(θ) are not always equal.

For example, when θ=45° the equation sin(2θ)=2sin(θ) becomes 1=√2 which is false.


Do not divide or multiply by sin because it's not a number. (It's a name.)


This way looks good. :smile:

'For example, when θ=45° the equation sin(2θ)=2sin(θ) becomes 1=√2 which is false.'
Could you simplify the point above, please?

 

[Dr.Peterson]

I have done below in two ways. please check my calculations below:
1. sin2θ = 1, (2) sinθ = sin 90,(2) sin θ/sin = sin 90 sin, 2θ/2 = 90/2, so θ = 45 degree
2. sinθ = 1, sin (90) = 1, so we get θ = 90, but here sin 2θ = 1, 2θ = 90, so θ = 45 degree

As has been said, you can't rewrite sin(2θ) as 2sin(θ); that just isn't true. In fact, you will eventually learn that sin(2θ) = 2sin(θ)cos(θ).

As I have said, you must never do something in mathematics just because it looks right to you. If you have not been taught that something is true, you can't use it.

Again, you were told some time ago that sin or tan is a function name, not a variable, so you can't "divide" by it -- writing sin θ/sin is utter nonsense.

Here is what we really do:

sin(2θ) = 1
arcsin(sin(2θ)) = arcsin(1)
2θ = 90°
2θ/2 = 90°/2
θ = 45°

(This is appropriate only on the assumption that you are looking for one (acute) solution, rather than all solutions.)

Your second work is close to this, but it is dangerous to change the meaning of θ in the middle of your work, so what I wrote is better form. I would say this, if you don't know about the arcsin (inverse sine) function yet:

sin(2θ) = 1
sin(2θ) = sin(90°)
2θ = 90°
2θ/2 = 90°/2
θ = 45°

Again, this is not sufficient if you are asked for all solutions, but is adequate if you just want a solution. If you have been given an exercise that asks for all solutions, let us know and we can show the appropriate work.

 

[mmm4444bot]

'For example, when θ=45° the equation sin(2θ)=2sin(θ) becomes 1=√2 which is false.'

Could you simplify the point above, please?

The main point is that sin(2θ) does not always equal 2∙sin(θ).

If you want to rewrite sin(2θ), then you must choose an expression that equals sin(2θ) for all possible values of θ.

(Look up the definition of "identity", in a trigonometry resource. You are expected to memorize some common identities.)

I showed you just one example where sin(2θ) ≠ 2∙sin(θ), and that was θ=45°.

sin(2θ) = sin(2∙45°) = sin(90°) = 1

2∙sin(θ) = 2∙sin(45°) = 2∙(√2/2) = √2

Clearly, sin(2θ) is not the same as 2sin(θ) when θ=45°

In fact, sin(2θ) and 2∙sin(θ) are different for almost all values of θ.

The double-angle identity for sine is: sin(2θ) = 2∙sin(θ)∙cos(θ) because these two expressions are equal for ALL values of θ.

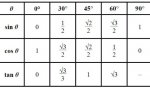
In addition to memorizing some of the identities shown on the list (linked above), you ought to also memorize sine and cosine values for some special angles (these angles are special because they appear often). :cool: