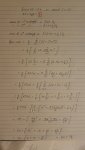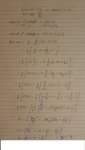Upper Sums - Generalized expression in terms of "n" - (est. of area under curve)

Hi, I've been stuck on this question enough time now that my brain has gone to soup. I'm not sure if I've over complicated for myself or am reading the question wrong. If anyone is able to spot where I'm going wrong a nudge in the right direction will be very much appreciated. I've uploaded a picture of one of the way's I've attempted to solve.. there's many other pages but generally am hitting the wall in the same part I feel (assuming my interpretation of what is being asked is what I'm trying to do!) - which i believe to be a generalized expression such that substituting for any n would give the sum of LHS of the rectangles.
Since LHS then I guess we want the x sub (i-1)th term but putting that into the function and expressing as sum of first n integers (pink box with #2) is causing brain.exe to crash.
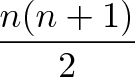
This was the question:
Consider function F(x)=25-5x on the interval [2,4] with "n" sub intervals. Calculate the Upper Sum giving the answer as an expression of "n" but no summation by using
results for "Important Sums" given from class.
The two "Important Sums" in the notes are outlined and marked 1 & 2 respectively in the attached image.

Hi, I've been stuck on this question enough time now that my brain has gone to soup. I'm not sure if I've over complicated for myself or am reading the question wrong. If anyone is able to spot where I'm going wrong a nudge in the right direction will be very much appreciated. I've uploaded a picture of one of the way's I've attempted to solve.. there's many other pages but generally am hitting the wall in the same part I feel (assuming my interpretation of what is being asked is what I'm trying to do!) - which i believe to be a generalized expression such that substituting for any n would give the sum of LHS of the rectangles.
Since LHS then I guess we want the x sub (i-1)th term but putting that into the function and expressing as sum of first n integers (pink box with #2) is causing brain.exe to crash.
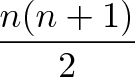
This was the question:
Consider function F(x)=25-5x on the interval [2,4] with "n" sub intervals. Calculate the Upper Sum giving the answer as an expression of "n" but no summation by using
results for "Important Sums" given from class.
The two "Important Sums" in the notes are outlined and marked 1 & 2 respectively in the attached image.