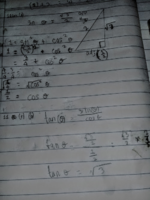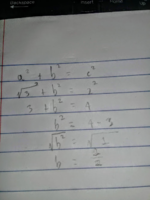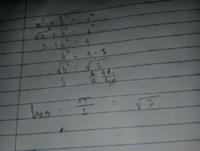I am confused. Since sinθ = √3 ÷ 2 , using the Pythagorean theorem to find for the missing side, I get the length as 1÷2
I know that the answer of (a) (i) = 1÷2 I don't know what steps to take to get it though.
And since we have all sides of the triangle then, tanθ = 2 ÷ 1/2, isn't it? but for (a) (ii) how is the Ans= √3

I know that the answer of (a) (i) = 1÷2 I don't know what steps to take to get it though.
And since we have all sides of the triangle then, tanθ = 2 ÷ 1/2, isn't it? but for (a) (ii) how is the Ans= √3