Dinoduck94
New member
- Joined
- May 15, 2019
- Messages
- 22
I have a coursework question that I'm hoping that I can get clarification on - please I don't want the answer, I just want clarification:
The question is below:
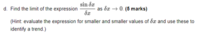
The partial derivatives here confused me.
Am I supposed to treat this essentially as sin(delta_x)/delta_x and then find a trend as I make delta_x closer and closer to 0; or is there something that I'm supposed to do with the partial derivatives?
Thanks
The question is below:
The partial derivatives here confused me.
Am I supposed to treat this essentially as sin(delta_x)/delta_x and then find a trend as I make delta_x closer and closer to 0; or is there something that I'm supposed to do with the partial derivatives?
Thanks
