Hckyplayer8
Full Member
- Joined
- Jun 9, 2019
- Messages
- 269
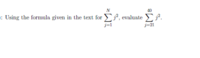
I searched and couldn't find anything with a capital N in the text, so I assume it is just a typo.
The aforementioned problem is just saying sum the values of j2, starting at 212 and ending at 402.
The text wants me to use the equation [n(n+1)(2n+1) / 6] but never really explains why (If it does, its not in a way I understand.)
When I see that I see the upper bound is replaced with 40 and the lower bound is replaced with 21.
So would my equation be [40(40+21)(2*40+21) / 6]?
