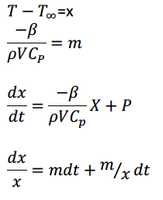Integral solving

[Minabb]

Hi all,

Can someone kindly please explain me how the equation (2) can be obtained from (1)?

I have attached the equations (1) and (2) in the attached pdf file.

Thanks a lot.

 

[Deleted member 4993]

Hi all,

Can someone kindly please explain me how the equation (2) can be obtained from (1)?

Please follow the rules of posting in this forum, as enunciated at:

READ BEFORE POSTING

Please share your work/thoughts about this assignment

Hint: Define new variable

S = T - \(\displaystyle T_{\infty}\)........ and define new constant

k = \(\displaystyle \frac{\beta}{\rho \ V \ C_p }\)

Then your DE (1) becomes:

\(\displaystyle \frac{dS}{dt} = -k*S + P \ \)....continue.....

 

[Minabb]

Thank for quick reply.

I replaced this part of equation with similar variable just you. Then I integral from both part of equation. can you guide me for the integral part and how to obtain equation 2 from 1.

Thanks

 

[Deleted member 4993]

Thank for quick reply.

I replaced this part of equation with similar variable just you. Then I integral from both part of equation. can you guide me for the integral part and how to obtain equation 2 from 1.

Thanks

Please show work - how did you integrate "both part of equation"? What did you get?

 

[Minabb]

Please show work - how did you integrate "both part of equation"? What did you get?

 

[Deleted member 4993]

View attachment 15451

You cannot integrate "directly". Have you taken a course in differential equations?

You have a first order differential equation.

You would need to solve it using "integrating factor".

 

[HallsofIvy]

View attachment 15451

You don't want your last step since you cannot integrate mdt+ (m/x)dt= m(1+ 1/x)dt with respect to t.

Instead, since this is a linear equation, there is a formula for an "integrating factor" that Subhotosh Kahn mentioned. I would be inclined to look at the "associated homogenous equation", \(\displaystyle \frac{dx}{dt}= \frac{-\beta}{\rho VC_p}x\). That is a "separable equation". We can "separate" it as \(\displaystyle \frac{dx}{x}= \frac{-\beta}{\rho VC_p} dt\). Integrating both sides, \(\displaystyle ln(x)= -\frac{\beta}{\rho VC_p}t+ C'\) where C' is the "constant of integration. Taking the exponential of both sides, \(\displaystyle x= C''e^{-\frac{\beta}{\rho VC_pt}}\) where \(\displaystyle C''= e^{C'}\).

Now look for a single solution to the entire equation. Since the "non-homogeneous" part is the constant, P, we look for a constant solution. Setting x= A, a constant, \(\displaystyle \frac{dx}{dt}= \frac{dA}{dt}= 0\) so the equation becomes \(\displaystyle 0= -\frac{\beta A}{\rho VC_p}+ P\). Solve that for A. \(\displaystyle \frac{\beta A}{\rho VC_p}= P\) so \(\displaystyle A=\frac{P\rho VC_P}{/beta}\).

Since this is a linear equation, we can add those together:
\(\displaystyle x(t)= C''e^{-\frac{\beta t}{\rho VC_p}}+ \frac{P\rho VC_p}{\beta}\).

 

[Minabb]

You don't want your last step since you cannot integrate mdt+ (m/x)dt= m(1+ 1/x)dt with respect to t.

Instead, since this is a linear equation, there is a formula for an "integrating factor" that Subhotosh Kahn mentioned. I would be inclined to look at the "associated homogenous equation", \(\displaystyle \frac{dx}{dt}= \frac{-\beta}{\rho VC_p}x\). That is a "separable equation". We can "separate" it as \(\displaystyle \frac{dx}{x}= \frac{-\beta}{\rho VC_p} dt\). Integrating both sides, \(\displaystyle ln(x)= -\frac{\beta}{\rho VC_p}t+ C'\) where C' is the "constant of integration. Taking the exponential of both sides, \(\displaystyle x= C''e^{-\frac{\beta}{\rho VC_pt}}\) where \(\displaystyle C''= e^{C'}\).

Now look for a single solution to the entire equation. Since the "non-homogeneous" part is the constant, P, we look for a constant solution. Setting x= A, a constant, \(\displaystyle \frac{dx}{dt}= \frac{dA}{dt}= 0\) so the equation becomes \(\displaystyle 0= -\frac{\beta A}{\rho VC_p}+ P\). Solve that for A. \(\displaystyle \frac{\beta A}{\rho VC_p}= P\) so \(\displaystyle A=\frac{P\rho VC_P}{/beta}\).

Since this is a linear equation, we can add those together:
\(\displaystyle x(t)= C''e^{-\frac{\beta t}{\rho VC_p}}+ \frac{P\rho VC_p}{\beta}\).

Thank you so much for your comprehensive explanation. I really appreciate your time.

if I understood correctly we separated the equation, my question is: why dx/dt=dA/dt=0?

 

[Deleted member 4993]

Thank you so much for your comprehensive explanation. I really appreciate your time.

if I understood correctly we separated the equation, my question is: why dx/dt=dA/dt=0?

The derivative of a constant (in this case A) is 0.