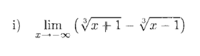You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
limit solving
- Thread starter acemi123
- Start date
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Rationalize by multiplying by \(\displaystyle \frac{{{{(x - 1)}^{2/3}} + \sqrt[3]{{x - 1}}\sqrt[3]{{x + 1}} + {{(x + 1)}^{2/3}}}}{{{{(x - 1)}^{2/3}} + \sqrt[3]{{x - 1}}\sqrt[3]{{x + 1}} + {{(x + 1)}^{2/3}}}}\)View attachment 15505I couldn't solve this questin. Can anyone help me, please?
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
It's pretty specific already. What do you get in the numerator? You should be able to multiply things like (a+b)(c+d+e) and then simplify.It sees more complicated than question
What must be the aproach to this kind of question? Can you be more specific pls?
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Rationalize by multiplying by \(\displaystyle \frac{{{{(x - 1)}^{2/3}} + \sqrt[3]{{x - 1}}\sqrt[3]{{x + 1}} + {{(x + 1)}^{2/3}}}}{{{{(x - 1)}^{2/3}} + \sqrt[3]{{x - 1}}\sqrt[3]{{x + 1}} + {{(x + 1)}^{2/3}}}}\)
To acemi123, If you are unprepared and/or unwilling to do simple algebra to work your assigned calculus questions then you are not going to pass the course. LOOK HERE. You can see that the product of the numerators is \(\displaystyle 2\).It sees more complicated than question
What must be the aproach to this kind of question? Can you be more specific pls?
Thus you handle the demonstrator \(\displaystyle \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt[3]{{x + 1}} - \sqrt[3]{{x - 1}}} \right)\left[ {{{(x - 1)}^{2/3}} + \sqrt[3]{{x - 1}}\sqrt[3]{{x + 1}} + {{(x + 1)}^{2/3}}} \right]\) as separate terms.
Again, if you are unwilling to do this sort of messy work, you have no hope of passing a calculus course.
a_guy_and_he_does_stuff
New member
- Joined
- Dec 13, 2019
- Messages
- 6
Not to bump a post which I have no business bumping, but I'd like to bump this post which I have no business bumping.
I've been looking over the answer provided by pka, and I'm actually somewhat confused as to the logical justification for rationalizing like this.
I took a look at this post early yesterday and saw pka's original answer. I did out the math by hand and got 2 as the product of the numerators. While I understand the process behind this and how we arrive there, I am not sure why it helps. I scoured over sources on evaluating limits via rationalization, though in most problems, they point to rationalizing the denominator, and in all cases I saw, both the numerator and the denominator need to have their limits taken so that the final fraction can be evaluated approaching infinity/negative infinity. This all pretty closely conforms to my education on the subject, but in this case, even though the numerator simplifies nicely, the denominator become an inoperable mess, and in my rather limited wisdom, it seems that we're back at square one.
I trust that your answer is right, but... I don't get it. I feel like this sentence is probably where my understanding breaks down. What do you mean by "handling the demonstrator ... (math) ... as separate terms"? Did you mean denominator?
I've been looking over the answer provided by pka, and I'm actually somewhat confused as to the logical justification for rationalizing like this.
I took a look at this post early yesterday and saw pka's original answer. I did out the math by hand and got 2 as the product of the numerators. While I understand the process behind this and how we arrive there, I am not sure why it helps. I scoured over sources on evaluating limits via rationalization, though in most problems, they point to rationalizing the denominator, and in all cases I saw, both the numerator and the denominator need to have their limits taken so that the final fraction can be evaluated approaching infinity/negative infinity. This all pretty closely conforms to my education on the subject, but in this case, even though the numerator simplifies nicely, the denominator become an inoperable mess, and in my rather limited wisdom, it seems that we're back at square one.
Thus you handle the demonstrator \(\displaystyle \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt[3]{{x + 1}} - \sqrt[3]{{x - 1}}} \right)\left[ {{{(x - 1)}^{2/3}} + \sqrt[3]{{x - 1}}\sqrt[3]{{x + 1}} + {{(x + 1)}^{2/3}}} \right]\) as separate terms.
I trust that your answer is right, but... I don't get it. I feel like this sentence is probably where my understanding breaks down. What do you mean by "handling the demonstrator ... (math) ... as separate terms"? Did you mean denominator?
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Here is a step by step complete solution. Learn from it.Not to bump a post which I have no business bumping, but I'd like to bump this post which I have no business bumping.
I've been looking over the answer provided by pka, and I'm actually somewhat confused as to the logical justification for rationalizing like this.
I took a look at this post early yesterday and saw pka's original answer. I did out the math by hand and got 2 as the product of the numerators. While I understand the process behind this and how we arrive there, I am not sure why it helps. I scoured over sources on evaluating limits via rationalization, though in most problems, they point to rationalizing the denominator, and in all cases I saw, both the numerator and the denominator need to have their limits taken so that the final fraction can be evaluated approaching infinity/negative infinity. This all pretty closely conforms to my education on the subject, but in this case, even though the numerator simplifies nicely, the denominator become an inoperable mess, and in my rather limited wisdom, it seems that we're back at square one.
I trust that your answer is right, but... I don't get it. I feel like this sentence is probably where my understanding breaks down. What do you mean by "handling the demonstrator ... (math) ... as separate terms"? Did you mean denominator?
Attachments
D
Deleted member 4993
Guest
than, it is too much for me
I have another one. Limit with square root are make me confuse . Is this also sould be solved according to Pka's answer?
View attachment 15548
Do similar thing:
multiply by one
or:
\(\displaystyle \frac{(\sqrt{x \ + \ 1}\ \ + \ \sqrt{x \ - \ 1)}}{(\sqrt{x \ + \ 1}\ \ + \ \sqrt{x \ - \ 1)}} \)
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
It sees more complicated than question
What must be the aproach to this kind of question? Can you be more specific pls?
I think someone in this thread should have taken the time to explain the basic concept, rather than just jumping on people who don't already know all about it.
We want the limit of [MATH]\sqrt[3]{x+1} - \sqrt[3]{x-1}[/MATH].
You presumably have seen problems like this with square roots, and learned to transform them by multiplying and dividing by the conjugate. (That's the method for handling the limit in post #5.) This is similar to rationalizing the denominator, but with a different goal, which is basically just to disrupt the expression enough to allow the limit to be taken. (The first time you try this, you're basically throwing a problem on the floor, hoping the pieces will be easier to handle. Once you've seen the trick once, it becomes a tool rather than just a random attempt to do something.)
The way the conjugate works with square roots is based on the fact that [MATH](a+b)(a-b) = a^2 - b^2[/MATH], so that if a and/or b is a square root, it will have been squared, and the square root is no more. This brings what were radicands out into the open where they can be worked with.
But this is a difference of cube roots rather than square roots, so the literal conjugate won't work. But the method of factoring a sum or difference of cubes does work: [MATH](a - b)(a^2 + ab + b^2) = a^3 - b^3[/MATH]. If a and b are cube roots, the result after multiplying has cubed them, and parts of the expression can be manipulated.
This was the reason for pka's suggestion in the first place. The rest of the work is ... just algebra.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
My question to you then is why should anyone of us think that a student who has been assigned this question would not have been introduced to the notation of rationalization? Moreover, reading the series of replies makes it perfectly clear that acemi123 is completely dismissive of my suggestion calling it in one case 'too complicated', 'more complicated than the original problem'. Now if this problem were given without having done the necessary background material then that is malpractice. Why should we not expect the student to work through class notes/textbooks to find a method of solution based on the suggestions?I think someone in this thread should have taken the time to explain the basic concept, rather than just jumping on people who don't already know all about it.
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
What a student given such a question probably has already been taught, but might not remember, is that \(\displaystyle (x- y)(x+ y)= x^2- y^2\), \(\displaystyle (x- y)(x^2+ xy+ y^2)= x^3- y^3\), and, in general, \(\displaystyle (x- y)(x^{n-1}+ x^{n-2}y+ x^{n-3}y^2+ \cdot\cdot\cdot+ x^2y^{n-3}+ xy^{n-2}+ y^{n-1})= x^n- y^n\).
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
If as posted the question were not an indeterminate form \(\displaystyle \infty-\infty\) I might agree with you on that possiblity.What a student given such a question probably has already been taught, but might not remember, is that \(\displaystyle (x- y)(x+ y)= x^2- y^2\), \(\displaystyle (x- y)(x^2+ xy+ y^2)= x^3- y^3\), and, in general, \(\displaystyle (x- y)(x^{n-1}+ x^{n-2}y+ x^{n-3}y^2+ \cdot\cdot\cdot+ x^2y^{n-3}+ xy^{n-2}+ y^{n-1})= x^n- y^n\).
But reading the poster's flippant replies makes me think otherwise.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
My goal is to help students, not to judge them. Last time I looked, the site wasn't called "freemathhumiliation.com".
For all we know, this may have been a challenge problem a step beyond what the OP has been taught, and the difference of cubes may not be an obvious connection to have made in their context.
But even if the OP wasn't deserving of a thoughtful explanation, I had the "guy's" post #10 in mind, which specifically asked for "the logical justification for rationalizing like this". Whether or not either of them has failed in their learning, why not explain it? I myself was a perfect student and never forgot anything, but I hear that's unusual ...
For all we know, this may have been a challenge problem a step beyond what the OP has been taught, and the difference of cubes may not be an obvious connection to have made in their context.
But even if the OP wasn't deserving of a thoughtful explanation, I had the "guy's" post #10 in mind, which specifically asked for "the logical justification for rationalizing like this". Whether or not either of them has failed in their learning, why not explain it? I myself was a perfect student and never forgot anything, but I hear that's unusual ...