fisher garrry
New member
- Joined
- Dec 11, 2017
- Messages
- 11
Below they are integrating a infinte long sheet of charge. I am wondering about how they integrate along x as the first part of a double integral. The point they want to find the field in is an upwards distance r from the sheet.
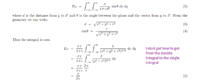
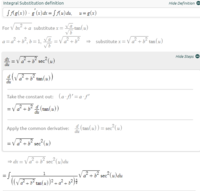
below is a calculation on how to integrate with respect to x in the double integral above
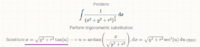
Can someone derive why
This is substitution - there is NO WHY to it. It makes the expression simpler to integrate!!
[MATH]x=\sqrt{y^2+r^2}tan(u)[/MATH]
I will add the rest of the integral since I have an issue in the end. The rest of the integral is as follows

Factor out 'x' from the denominator and cancel out the x in the numerator - then apply limits x \(\displaystyle \to \pm \infty \)
I don't get the next step where they add the integration limits:

How do they get this definite integral [MATH]\frac{x}{(y^2+r^2)\sqrt{x^2+y^2+r^2}}+C[/MATH] from [MATH]-\infty[/MATH] to [MATH]\infty[/MATH] to become [MATH]\frac{2}{y^2+r^2}[/MATH]?
Explained above.
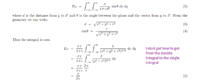
below is a calculation on how to integrate with respect to x in the double integral above
Can someone derive why
This is substitution - there is NO WHY to it. It makes the expression simpler to integrate!!
[MATH]x=\sqrt{y^2+r^2}tan(u)[/MATH]
I will add the rest of the integral since I have an issue in the end. The rest of the integral is as follows

Factor out 'x' from the denominator and cancel out the x in the numerator - then apply limits x \(\displaystyle \to \pm \infty \)
I don't get the next step where they add the integration limits:

How do they get this definite integral [MATH]\frac{x}{(y^2+r^2)\sqrt{x^2+y^2+r^2}}+C[/MATH] from [MATH]-\infty[/MATH] to [MATH]\infty[/MATH] to become [MATH]\frac{2}{y^2+r^2}[/MATH]?
Explained above.
Last edited: