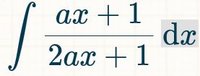You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Integration problem
- Thread starter Stef95
- Start date
- Joined
- Nov 24, 2012
- Messages
- 3,021
What I would do next is let:
[MATH]u=2ax+1\implies du=2a\,dx[/MATH]
And so now we have:
[MATH]\frac{1}{4a}\int 1+\frac{1}{u}\,dx=\frac{1}{4a}(u+\ln(u))+C[/MATH]
Now back substitute for \(u\):
[MATH]\int\frac{ax+1}{2ax+1}\,dx=\frac{1}{4a}(2ax+\ln(2ax+1))+C[/MATH]
Note: the constant that resulted in the back-substitution was "absorbed" into the constant of integration.
[MATH]u=2ax+1\implies du=2a\,dx[/MATH]
And so now we have:
[MATH]\frac{1}{4a}\int 1+\frac{1}{u}\,dx=\frac{1}{4a}(u+\ln(u))+C[/MATH]
Now back substitute for \(u\):
[MATH]\int\frac{ax+1}{2ax+1}\,dx=\frac{1}{4a}(2ax+\ln(2ax+1))+C[/MATH]
Note: the constant that resulted in the back-substitution was "absorbed" into the constant of integration.
And so now we have:
The natural logarithms in the antiderivatives get used with the absolute
value bars.
[MATH] ... \ = \ \frac{1}{4a}(u+\ln|u|) \ + \ C[/MATH]
Now back substitute for \(u\):
[MATH]\int\frac{ax+1}{2ax+1}\,dx \ = \ \frac{1}{4a}(2ax+\ln|2ax+1|) \ + \ C[/MATH]