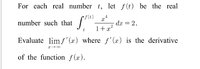You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How to solve this example?
- Thread starter Asad
- Start date
D
Deleted member 4993
Guest
View attachment 15815
Please follow the rules of posting in this forum, as enunciated at:
READ BEFORE POSTING
Please share your work/thoughts about this assignment.
Hint: substitute:
x^4 = x^2 * (1+x^2) - (x^2+1) +1
and solve the integration first.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
To Asad, Is this a question which is actually published in some textbook?
If it is, will you kindly tell us to name of the text and its author(s).
Parts of the question are relatively straightforward: the antiderivative is \(\displaystyle \int {\frac{{{x^4}}}{{1 + {x^2}}}dx} = \frac{{{x^3}}}{3} - x + \arctan (x)\)
And if it were \(\displaystyle T(t) = \int_t^{f(t)} {\frac{{{x^4}}}{{1 + {x^2}}}dx} \) then \(\displaystyle T'(t) = f'(t)\frac{{(f{{(t)}^4})}}{{1 + {{(f(t))}^2}}} - \frac{{{{(t)}^4}}}{{1 + {{(t)}^2}}}\)
But as stated, there seems to be a mix up of concepts.
If it is, will you kindly tell us to name of the text and its author(s).
Parts of the question are relatively straightforward: the antiderivative is \(\displaystyle \int {\frac{{{x^4}}}{{1 + {x^2}}}dx} = \frac{{{x^3}}}{3} - x + \arctan (x)\)
And if it were \(\displaystyle T(t) = \int_t^{f(t)} {\frac{{{x^4}}}{{1 + {x^2}}}dx} \) then \(\displaystyle T'(t) = f'(t)\frac{{(f{{(t)}^4})}}{{1 + {{(f(t))}^2}}} - \frac{{{{(t)}^4}}}{{1 + {{(t)}^2}}}\)
But as stated, there seems to be a mix up of concepts.
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,702
I would expect \(\displaystyle \lim_{x\to\infty} f'(x)=1\). I don't know how to formally prove this, but I'll explain my thinking in words.
After applying the integral limits (assuming pka's integral is correct) you end up with the following implicit equation:-
Using y for f(x)... \(\displaystyle \color{red}\frac{y^3}{3} \color{black} -y+\tan^{-1}\left(y\right)=2+\color{red}\frac{x^3}{3} \color{black}-x+\tan^{-1}\left(x\right)\)
The terms in red become dominant as x gets large, therefore the equation becomes more like \(\displaystyle y=x\) for large x. And in this situation the derivative would be 1. But I don't know how you would express this in a mathematically correct way.
After applying the integral limits (assuming pka's integral is correct) you end up with the following implicit equation:-
Using y for f(x)... \(\displaystyle \color{red}\frac{y^3}{3} \color{black} -y+\tan^{-1}\left(y\right)=2+\color{red}\frac{x^3}{3} \color{black}-x+\tan^{-1}\left(x\right)\)
The terms in red become dominant as x gets large, therefore the equation becomes more like \(\displaystyle y=x\) for large x. And in this situation the derivative would be 1. But I don't know how you would express this in a mathematically correct way.
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
After I posted I realized that although \(\displaystyle \frac{x^4}{1+x^2}\) is continuous function, there is absolutely no reason to assume that given the way \(\displaystyle f(t)\) is defined that it is also differentiable. I have worked with the theory of the integral my entire professional life. But I have never seen any thing like this question. That is why I asked about its source. I cannot think of an adequate description for what to me is like a mixed metaphor. I really do look forward to Asad's response.After applying the integral limits (assuming pka's integral is correct) you end up with the following implicit equation:-
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,702
I just did an implicit plot of f(x), shown in red below, and it does seem differentiable in this case. It goes near vertical at approx (-2.068, 0) but seems continuous.
The green line shows y=x.
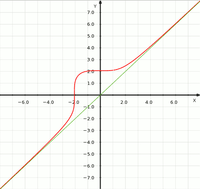
I've never seen a question like this before either. The way that f(x) is defined is quite interesting. Thinking about it graphically it returns an x-coordinate to the right of the passed in x-coordinate such that there are two +ve units of area underneath the curve \(\displaystyle \frac{x^4}{1+x^2}\) between the two x locations. I guess this returns a unique value because \(\displaystyle \frac{x^4}{1+x^2}\) stays +ve.
The green line shows y=x.

I've never seen a question like this before either. The way that f(x) is defined is quite interesting. Thinking about it graphically it returns an x-coordinate to the right of the passed in x-coordinate such that there are two +ve units of area underneath the curve \(\displaystyle \frac{x^4}{1+x^2}\) between the two x locations. I guess this returns a unique value because \(\displaystyle \frac{x^4}{1+x^2}\) stays +ve.
Cubist
Senior Member
- Joined
- Oct 29, 2019
- Messages
- 1,702
\(\displaystyle
f^\prime(t) = \dfrac{t^2}{\left(6+t^3\right)^{2/3}}
\)
And from there it is easy to prove \(\displaystyle \lim_{t\to \infty} f^\prime(t)=1 \).
This seems a great way of proving the result, but does not seem in the spirit of the original question which explicitly asks for the integral of \(\displaystyle \frac{x^4}{1+x^2} \).