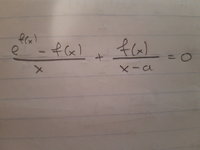At least one soution in a no continuous

E

eleni24

New member
Joined
Apr 10, 2020
Messages
10
Hey guys
The exercise in which I'm facing a problem is the following:
f(x)= 1/x ,x<0
ln(e^x+x) ,x<=0

It asks you to show that for every value of a>0 ,the equation

(e^f(x)-f(x))/x +f(x)/(x-a)=0
has at least one solution. My problem is that the function is not continuous at 0 so any theorem i can think of doesn't work. Any idea?
Thanks in advance
 
Last edited:
eleni24 said:
Hey guys
The exercise in which I'm facing a problem is the following:
f(x)= 1/x ,x<0
ln(e^x+x) ,x<=0
Click to expand...

Hi, to make the question clear, I assume that this is f(x)...

[math]f(x)=\begin{cases} \frac{1}{x} & x<0\\ ln(e^{x}+x) & \color{red}x\geqslant 0 \end{cases}[/math]
 
I suspect that Cubist's correction is spot on . However, there is no \(\large\bf{a}\) in the correction as there is in the PO.
 
I don't see a problem here, for the function definition anyway. The value of a is only a feature of the equation that needs to be solved.

-Dan
 
Cubist said:
Hi, to make the question clear, I assume that this is f(x)...

[math]f(x)=\begin{cases} \frac{1}{x} & x<0\\ ln(e^{x}+x) & \color{red}x\geqslant 0 \end{cases}[/math]
Click to expand...
Yes this is f(x). I tried to paste it from word but it didn't work out.
 
topsquark said:
I don't see a problem here, for the function definition anyway. The value of a is only a feature of the equation that needs to be solved.

-Dan
Click to expand...
Exactly. The letter a is just a parameter. It doesn't have to do with the function.
 
pka said:
I suspect that Cubist's correction is spot on . However, there is no \(\large\bf{a}\) in the correction as there is in the PO.
Click to expand...
Letter a is just a paremeter given in the equation that needs to be solved. Not a part of the function.
 
To make it clear, to correct f(x) type is what Cubist posted, while the equation we have to prove that has at least one solution in (0,a) is
in the file I attached here.
.(My fault, I forgot to tell you the interval in which we are searching for the solution). Hope I made it all clear. If any mistake please tell me.
 

Attachments

  • 20200415_125643.jpg
    20200415_125643.jpg
    4.8 MB · Views: 2
@eleni24 have you noticed that the equation always uses f(x). It does NOT use f(x+1), nor f(y) etc. Only f(x).

What does this tell us? Does this mean that it's possible to rewrite the equation, twice, once for the case when x<0 and once for x≥0?
 
eleni24 said:
To make it clear, to correct f(x) type is what Cubist posted, while the equation we have to prove that has at least one solution in (0,a) is
in the file I attached here.
.(My fault, I forgot to tell you the interval in which we are searching for the solution). Hope I made it all clear. If any mistake please tell me.
Click to expand...

The interval (0,a) seems important; doesn't it allow you to consider only positive x, and therefore ignore the negative case in the definition of f?
 
You must log in or register to reply here.
Top