MooreLikeMike
New member
- Joined
- Nov 10, 2020
- Messages
- 13
Hello,
I'm having a hard time figuring out this question: find the value of k so that f(x) = k/(x+1)^2 for x greater than or equal to 1 and less than or equal to 2 is a probability function.
I know that to be a pdf 1) f(x) must be greater than or equal to 1, and 2) the integral of f(x)dx from "a" to "b" must equal 1.
So to solve the question, I found the integral of k/(x+1)^2 and evaluated it at x =2 then subtracted that for when x =1 and got -6/5
It would be great if someone could tell me where I went wrong so that I can try to move in the right direction.
Thank you!
(the work that I've done so far is attached to this)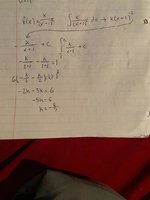
I'm having a hard time figuring out this question: find the value of k so that f(x) = k/(x+1)^2 for x greater than or equal to 1 and less than or equal to 2 is a probability function.
I know that to be a pdf 1) f(x) must be greater than or equal to 1, and 2) the integral of f(x)dx from "a" to "b" must equal 1.
So to solve the question, I found the integral of k/(x+1)^2 and evaluated it at x =2 then subtracted that for when x =1 and got -6/5
It would be great if someone could tell me where I went wrong so that I can try to move in the right direction.
Thank you!
(the work that I've done so far is attached to this)