homeschool girl
Junior Member
- Joined
- Feb 6, 2020
- Messages
- 123
The question:
A regular dodecagon [MATH]P_1 P_2 P_3 \dotsb P_{12}[/MATH] is inscribed in a circle with radius [MATH]1.[/MATH] Compute
\[(P_1 P_2)^2 + (P_1 P_3)^2 + \dots + (P_{11} P_{12})^2.\]
(The sum includes all terms of the form [MATH](P_i P_j)^2,[/MATH] where [MATH]1 \le i < j \le 12.[/MATH])
Where I'm stuck:
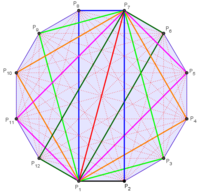
I drew out the dodecagon and labeled all the points, I figured out how to find lines like [MATH]\overline{P_1P_4}[/MATH] that form right angles and are equal to [MATH] \sqrt{r^2+r^2}= \sqrt{1+1}=\sqrt{2}[/MATH], and lines like [MATH]\overline{P_1P_7}[/MATH] that form straight lines and are equal to [MATH] r+r = 2[/MATH], but I'm unsure on how to find the other types of lines.
A regular dodecagon [MATH]P_1 P_2 P_3 \dotsb P_{12}[/MATH] is inscribed in a circle with radius [MATH]1.[/MATH] Compute
\[(P_1 P_2)^2 + (P_1 P_3)^2 + \dots + (P_{11} P_{12})^2.\]
(The sum includes all terms of the form [MATH](P_i P_j)^2,[/MATH] where [MATH]1 \le i < j \le 12.[/MATH])
Where I'm stuck:
I drew out the dodecagon and labeled all the points, I figured out how to find lines like [MATH]\overline{P_1P_4}[/MATH] that form right angles and are equal to [MATH] \sqrt{r^2+r^2}= \sqrt{1+1}=\sqrt{2}[/MATH], and lines like [MATH]\overline{P_1P_7}[/MATH] that form straight lines and are equal to [MATH] r+r = 2[/MATH], but I'm unsure on how to find the other types of lines.