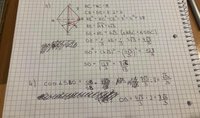Hi! I am struggling with this task: " find the sine of the angle that forms the sidewall of this pyramid with the base plane ". This pyramid is a
tetrahedron and it's edge equals to 8.
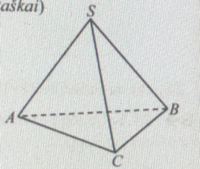
As I understood, I have to find the sine of the angle SBC or am I mistaken? Moreover, to find a sine shouldn't it be a right triangle? I am sorry, I really do not have any concrete ideas. Could you, please give me any hints? Thank you.
tetrahedron and it's edge equals to 8.

As I understood, I have to find the sine of the angle SBC or am I mistaken? Moreover, to find a sine shouldn't it be a right triangle? I am sorry, I really do not have any concrete ideas. Could you, please give me any hints? Thank you.