Combination problem: Geometry and probably some calc too...

[colgate2004]

Hi all,

Thanks in advance for the help with this. This may be a more involved/difficult one than is common here.

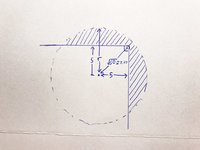
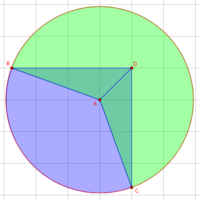
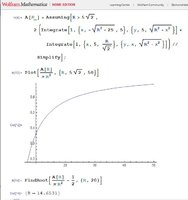
A circle is centered a distance of 5 (feet, inches, whatever) away from both of two perpendicular lines (therefore sqrt50 or ~7.07 away from their intersection). Find the radius such that half of the area of the circle (0.5A) lies on one side of the lines, with the other 50% lying on the other side.

(Diagram attached)

I'm completely stumped here. Help appreciated!

 

[colgate2004]

This is probably more calc than geometry... should I repost it in the calculus board?

 

[tkhunny]

For starters, "whatever" doesn't cut it. What is "r". Is it always consistent with your "5 whatever"? The problem needs a Domain.

 

[colgate2004]

“r” is the radius of the circle, i.e. what we’re trying to solve for, in the same unit we choose for the distance of 5 to be in. If you need a unit, let’s pick... meters. So the center is 5 meters from each line, and we’re solving for the radius, in meters.

 

[Dr.Peterson]

First, you need to make a formula for the area of one of the two parts; I'd do the "inside". Then you can set that equal to half the area of the circle and solve for r; I expect that you will be approximating that.

Here is one way to make the formula:



You want the sum of the area of the sector in blue, and the two triangles in dark green. (If you wanted the outside area, you could use a sector minus the triangles.)

 

[Romsek]

[MATH]\large \displaystyle A = 2\left(\int \limits_{-\sqrt{R^2 - 25}}^5 \int \limits_5^{\sqrt{R^2-x^2}} ~dy~dx + \int \limits_5^{\frac{R}{\sqrt{2}}} \int \limits_x^{\sqrt{R^2 - x^2}}~dy~dx\right)[/MATH]
[MATH]\dfrac{A}{\pi R^2} = \dfrac 1 2 \Rightarrow R \approx 14.65[/MATH]
A(R) does have a closed form but it's nasty

[MATH]A(R) = \dfrac{3 \pi R^2}{4}-5 \left(\sqrt{R^2-25}+5\right)+R^2 \left(-\tan ^{-1}\left(\dfrac{5}{\sqrt{R^2-25}}\right)\right)[/MATH]

 

[tkhunny]

“r” is the radius of the circle, i.e. what we’re trying to solve for, in the same unit we choose for the distance of 5 to be in. If you need a unit, let’s pick... meters. So the center is 5 meters from each line, and we’re solving for the radius, in meters.

I was just momentarily concerned about r = 3, say. Are you SURE there is ALWAYS a solution?

 

[colgate2004]

First, you need to make a formula for the area of one of the two parts; I'd do the "inside". Then you can set that equal to half the area of the circle and solve for r; I expect that you will be approximating that.

Here is one way to make the formula:

View attachment 24382

You want the sum of the area of the sector in blue, and the two triangles in dark green. (If you wanted the outside area, you could use a sector minus the triangles.)

Dr. Peterson,

That is brilliant. It never would have occurred to me to break the area into three parts like that. I think I can come up with a formula for that inside area as a sum of those three parts you illustrated. Thank you!!!

 

[colgate2004]

[MATH]\large \displaystyle A = 2\left(\int \limits_{-\sqrt{R^2 - 25}}^5 \int \limits_5^{\sqrt{R^2-x^2}} ~dy~dx + \int \limits_5^{\frac{R}{\sqrt{2}}} \int \limits_x^{\sqrt{R^2 - x^2}}~dy~dx\right)[/MATH]
[MATH]\dfrac{A}{\pi R^2} = \dfrac 1 2 \Rightarrow R \approx 14.65[/MATH]
A(R) does have a closed form but it's nasty

[MATH]A(R) = \dfrac{3 \pi R^2}{4}-5 \left(\sqrt{R^2-25}+5\right)+R^2 \left(-\tan ^{-1}\left(\dfrac{5}{\sqrt{R^2-25}}\right)\right)[/MATH]
View attachment 24383

Romesk,
Thank you very much for what looks like a lot of work. My calculus, unfortunately, is *very* lacking and I’m struggling to even make sense of your work there! But your answer of 14.65 aligns very closely with my expected value, so I’m sure your work is correct. Thank you!