alwaysthefangirl
New member
- Joined
- Feb 1, 2021
- Messages
- 1
Here is the problem:
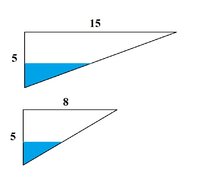
A swimming pool is 15 feet wide, 8 feet long, and 5 feet deep at one end. The depth gradually decreases to 0 at the other end (as shown in the picture). Water is being added to the pool at the rate of 10 cubic feet per minute. Find the rate at which the water level is rising when there are 300 cubic feet of water in the pool. Hint, think similar triangles and a triangular prism of water.
I am so lost on where to start with this, but here is what I have:
- V(of the water)=(1/2)(l*w*h)
- I think V'(of the water)=10
- I think that V of the water at the end is 300
- V(of the swimming pool)=600
I really dont have anything else
I usually am ok with related rates, but this one makes absolutly no senseeeeeeeeee. Please help!!!!!!
A swimming pool is 15 feet wide, 8 feet long, and 5 feet deep at one end. The depth gradually decreases to 0 at the other end (as shown in the picture). Water is being added to the pool at the rate of 10 cubic feet per minute. Find the rate at which the water level is rising when there are 300 cubic feet of water in the pool. Hint, think similar triangles and a triangular prism of water.
I am so lost on where to start with this, but here is what I have:
- V(of the water)=(1/2)(l*w*h)
- I think V'(of the water)=10
- I think that V of the water at the end is 300
- V(of the swimming pool)=600
I really dont have anything else
I usually am ok with related rates, but this one makes absolutly no senseeeeeeeeee. Please help!!!!!!