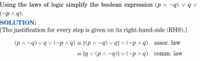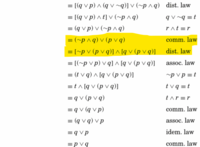bushra1175
Junior Member
- Joined
- Jun 14, 2020
- Messages
- 59
Here are the laws in the textbook:

The distributive law was applied to the upper statement, resulting in the lower one:
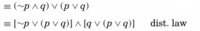
I have stared at this for a long time and the transformation looks completely unrelated to the distributive law illustrated in the texbook. This snipet is part of a simplification of the below logic statement. I understand everything up until the highlighted part:
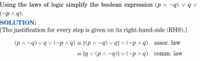
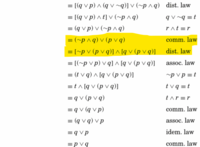

The distributive law was applied to the upper statement, resulting in the lower one:
I have stared at this for a long time and the transformation looks completely unrelated to the distributive law illustrated in the texbook. This snipet is part of a simplification of the below logic statement. I understand everything up until the highlighted part: