Berthin Alexander
New member
- Joined
- Jun 16, 2020
- Messages
- 14
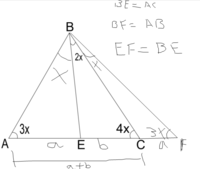
Can you explain the thinking behind your markings, including what the green line is? Some (or maybe all) of them are wrong (such as the two apparently equal angles into which you divided 4x, unequally).Find "x". If AC=BC.
I tried to find congruence. I do not know what more to do. Could you give me ideas please?
View attachment 26076
the green line is a bisector.Can you explain the thinking behind your markings, including what the green line is? Some (or maybe all) of them are wrong (such as the two apparently equal angles into which you divided 4x, unequally).
Use what you do know. You knew to make an angle bisector, which is also the perpendicular bisector of AB. So the two angles on either side of that are both 2x, right?the green line is a bisector.
Draw the line of that green bisector trying to find congruence of triangles.
I'm honestly not sure how to solve that problem so I posted it on this page
Because \(AC=BC\) is it true that \(\Delta ACB\) is isosceles ?Find "x". If AC=BC.
View attachment 26075
----
I tried to find congruence. I do not know what more to do. Could you give me ideas please?
Yes, you just need to look at the big triangle ABC. As has been said, [MATH]\bigtriangleup[/MATH] ABC is isosceles,m(∠CAB)=m(∠CBA)
I want to apologize to all of you. Mispublish the geometry problem. It is actually AC = BE.Because \(AC=BC\) is it true that \(\Delta ACB\) is isosceles ?
If so, does that mean that \(m(\angle CAB)=m(\angle CBA)~?\)
What can you now conclude about \(3x+4x+2x+?=\Large ?\)
I want to apologize to all of you. Mispublish the geometry problem. It is actually AC = BE.Yes, you just need to look at the big triangle ABC. As has been said, [MATH]\bigtriangleup[/MATH] ABC is isosceles,
so you know (in terms of x) the three angles in [MATH]\bigtriangleup[/MATH] ABC: 4x, 3x, ?
and you know what the three angles in a triangle add up to.
I want to apologize to all of you. Mispublish the geometry problem. It is actually AC = BE.I think you are making this a lot harder than it is. If AC=BC, then triangle ABC is isosceles. Which 2 angles are congruent?
It gives the same answer - and AC=BC too.I want to apologize to all of you. Mispublish the geometry problem. It is actually AC = BE.
but I already solved it on my own. Anyway, thank you very much for your help and your time. you are good people
@Berthin Alexander
It gives the same answer - and AC=BC too.
It would be interesting to see your solution.