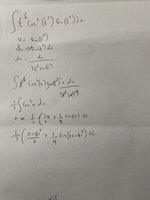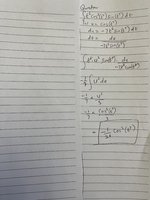Hi,
I have tried integrating this function using integration by part but seem to behave like an endless cycle of sin(t)cos(t) that needs another integration by part. the function is the integration of t^6cos^2(t^7)sin(t^7).
I made u=t^7 and got the integration of cos^2(u)sin(u)du.
I used integration udv=uv - integration vdu but ended up with a cycle of the integration of the product of sine cosine needing another udv method.
I then tried substituting cos^2(u) with 1-sin^2(u) which worked well until I got to the point 1/7 multiplied by the integration of sin(u) - sin^3(u). I could not go past this stage. Can somebody help, please?
I really did not want to seek help but couldn't get past this stage. The reason being I do not want to come here seeking only help especially because I was asked to show if I really did attempt to solve a problem yesterday and referred back to the rules of the forum. I did everything I could before coming here.
Also, sorry, I do not have an app to type this more accurately (mathematically). In addition, my phone does not connect with my computer so if I take a shot of the handwritten work, I have to send it to email, then download, and then attach it before sending. It is a lot of processes. I hope you can understand the questions.
Many thanks.
I have tried integrating this function using integration by part but seem to behave like an endless cycle of sin(t)cos(t) that needs another integration by part. the function is the integration of t^6cos^2(t^7)sin(t^7).
I made u=t^7 and got the integration of cos^2(u)sin(u)du.
I used integration udv=uv - integration vdu but ended up with a cycle of the integration of the product of sine cosine needing another udv method.
I then tried substituting cos^2(u) with 1-sin^2(u) which worked well until I got to the point 1/7 multiplied by the integration of sin(u) - sin^3(u). I could not go past this stage. Can somebody help, please?
I really did not want to seek help but couldn't get past this stage. The reason being I do not want to come here seeking only help especially because I was asked to show if I really did attempt to solve a problem yesterday and referred back to the rules of the forum. I did everything I could before coming here.
Also, sorry, I do not have an app to type this more accurately (mathematically). In addition, my phone does not connect with my computer so if I take a shot of the handwritten work, I have to send it to email, then download, and then attach it before sending. It is a lot of processes. I hope you can understand the questions.
Many thanks.
Last edited: