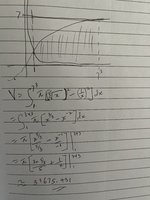Solid of Revolution Help needed

[dBanji]

Hello I need help figuring out what region bounded by four curves I’m required to find. I have attached the question and an attempt suggested by someone because i had no clue how to proceed. I can use some help from you guys. Many thanks.

 

[Dr.Peterson]

Please don't double-post.

As I said on the other thread, I don't understand the problem either. Do you have anything to help us interpret it, such as a supposedly correct answer, or a hint or example they provide?

If there are similar problems, or especially a worked example with the same oddity, we'll want to see them.

 

[dBanji]

Sure, there are similar questions in the text book exercise which only differ by just the y value. The problem in question has y-value of 7 while others have y values of 4 and 8. Every other part of the questions are the same. For y=8, the answer is 72pi/5. And the one with y=2, the answer is 52pi/5. How they got that I do not know.

 

[dBanji]

Please don't double-post.

As I said on the other thread, I don't understand the problem either. Do you have anything to help us interpret it, such as a supposedly correct answer, or a hint or example they provide?

If there are similar problems, or especially a worked example with the same oddity, we'll want to see them.

There was no worked example just answers to the exercise

 

[Dr.Peterson]

For y=8, the answer is 72pi/5. And the one with y=2, the answer is 52pi/5. How they got that I do not know.

That's exactly what we need, because we can try different interpretations of those problems and see which gives those results. Have you tried finding the volumes when different pieces of the graph are revolved around the axis?



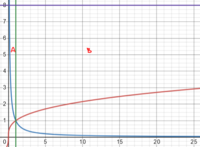
I expect it to be A, B, or their union. Give it a try, and I'll do the same if I run out of other things to do.

 

[dBanji]

That's exactly what we need, because we can try different interpretations of those problems and see which gives those results. Have you tried finding the volumes when different pieces of the graph are revolved around the axis?

View attachment 26810

I expect it to be A, B, or their union. Give it a try, and I'll do the same if I run out of other things to do.

That’s the exact graph I got. It is difficult to get a point where all of them meet. There is no single area where they all meet. If you choose A you would leave out B and vice versa. Yet there is no point where those two meet. The red line did meet the y=7 line somewhere farther away from the origin though, but equating both equations to get point of intersection did not work for me.

 

[Dr.Peterson]

That’s the exact graph I got. It is difficult to get a point where all of them meet. There is no single area where they all meet. If you choose A you would leave out B and vice versa. Yet there is no point where those two meet. The red line did meet the y=7 line somewhere farther away from the origin though, but equating both equations to get point of intersection did not work for me.

Huh? Who said anything about regions meeting at a point?

Please do what I suggested. Find what you get if you suppose that the poorly-written question meant only region A, or only region B. Once we get those, we can try to figure out what they really meant.

 

[Dr.Peterson]

Sure, there are similar questions in the text book exercise which only differ by just the y value. The problem in question has y-value of 7 while others have y values of 4 and 8. Every other part of the questions are the same. For y=8, the answer is 72pi/5. And the one with y=2, the answer is 52pi/5. How they got that I do not know.

If I take the suggestion in the other thread, the second example looks like this:


But I get a smaller volume than 52pi/5, namely 12pi/5. I could be wrong, so check it. And keep trying other possibilities.

 

[dBanji]

If I take the suggestion in the other thread, the second example looks like this:
View attachment 26817

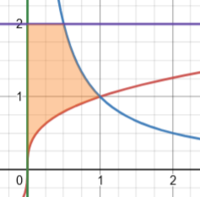
But I get a smaller volume than 52pi/5, namely 12pi/5. I could be wrong, so check it. And keep trying other possibilities.

Thank you for getting back. The correct answer is 62`pi`/5. The answer for the y=2 from the textbook was wrong I guess as the online exercise platform generated a different answer for y=2. The answer for y=2 from the practice question is 12`pi`/5, for y=3 it's 22`pi`/5, for y=4 it is 32`pi`/5, for y=5 it is 42`pi`/5, for y=6 it's 52`pi`/5, for y=8 it's 72`pi`/5, and for y=9, it's 82`pi`/5. Seeing this pattern, I chose 62`pi`/5 for y=7 and it was correct. I still do not know how they arrived at the answer. I tried to pay an online math tutor to walk me through but none of them could get it right. Another coursemate complained about the same question that she tried several tutors but none could get it right. I reached out to the professor if she could solve a similar problem and show me how. I'm still waiting on her. I will let you know as soon as she gets back to me.

Thank you for your time and help.

 

[Dr.Peterson]

The answer for y=2 from the practice question is 12πpi/5

You did see that I got that answer in post #8, right?

I still do not know how they arrived at the answer.

I used the washer method in two parts; you could also use cylindrical shells in two parts.

Please show your attempt, now that we seem to know how to correct the statement of the problem.