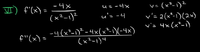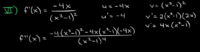I'm following a tutorial on curve sketching and I got stuck on simplifying the second derivative. The answer they got is f" = [math]12x[/math]+[math]4[/math] / [math](x^2[/math] [math]-1)[/math] [math]^3[/math]
I'm not sure how they are getting that answer. Can someone explain?
I'm not sure how they are getting that answer. Can someone explain?