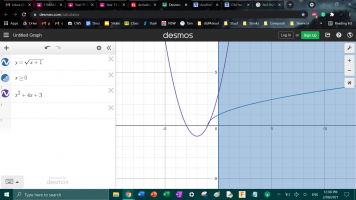
let f(x) = √(x+1) for x>=0
i. state the range of f(x), and I said that y >= 1
but for ii. it's asking me to let g(x) = x^2 +4x +3, where x<= c and c<= 0. Find the largest possible value of c such that the range of g(X) is a subset of the domain of f(x).
i. state the range of f(x), and I said that y >= 1
but for ii. it's asking me to let g(x) = x^2 +4x +3, where x<= c and c<= 0. Find the largest possible value of c such that the range of g(X) is a subset of the domain of f(x).