You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Triangle circumscribes four circles
- Thread starter westin
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,852
Mark points of tangency, and draw in all the radii you can find!View attachment 29255
Hi,
I do not know how to start the above question. Can someone give me some pointers?
The answer is 11
Thanks,
Chris
Then look for equilateral or 30-60-90 triangles, and start marking the lengths of their sides.
got it. thank you.
triangle EFG is a 90-60-30 triangle. angle EFG is 60 because triangle ABC is an equilateral triangle.
side EF = 3 + 3/root 3
using cos 60 = 1/2 = (3+3 /root 3)/FG
then FG = 6 + 6/root 3 = 6 + 2 root 3
where a = 6, b = 2 and c =3 then answer = 11.
Thanks again for the help!!!!
triangle EFG is a 90-60-30 triangle. angle EFG is 60 because triangle ABC is an equilateral triangle.
side EF = 3 + 3/root 3
using cos 60 = 1/2 = (3+3 /root 3)/FG
then FG = 6 + 6/root 3 = 6 + 2 root 3
where a = 6, b = 2 and c =3 then answer = 11.
Thanks again for the help!!!!
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
You found that one angle is 60. How do you know the other angles are 90 and 30?got it. thank you.
triangle EFG is a 90-60-30 triangle. angle EFG is 60 because triangle ABC is an equilateral triangle.
side EF = 3 + 3/root 3
using cos 60 = 1/2 = (3+3 /root 3)/FG
then FG = 6 + 6/root 3 = 6 + 2 root 3
where a = 6, b = 2 and c =3 then answer = 11.
Thanks again for the help!!!!
How do you know EF's length?
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 618
Beer induced ramblings follow.
Can you post your work?
Others can learn from it.
Your answers seem to be correct.got it. thank you.
triangle EFG is a 90-60-30 triangle. angle EFG is 60 because triangle ABC is an equilateral triangle.
side EF = 3 + 3/root 3
using cos 60 = 1/2 = (3+3 /root 3)/FG
then FG = 6 + 6/root 3 = 6 + 2 root 3
where a = 6, b = 2 and c =3 then answer = 11.
Thanks again for the help!!!!
Can you post your work?
Others can learn from it.
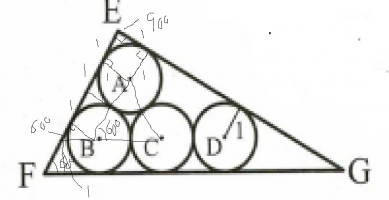
hi, based on above drawing. since the shape of the vertex E is a square, we can deduce that angle E is 90 degrees. since triangle ABC is an equilateral triangle, then we can deduce that angle ABC is 60 degrees which meant angle EFG is also 60 degrees. by using 30-60-90 rule or sin/cos/tan, we can find out the sides of EF which is 3 plus 3/root 3. and then using 30-60-90 rule or cos 60, we can find FG. my previous post have more detail formulas. thanks!
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
Sorry, you can't assume that the angle E is 90 degrees based on the diagram. If it's not given that it's 90, then don't assume that it's 90.View attachment 29261
hi, based on above drawing. since the shape of the vertex E is a square, we can deduce that angle E is 90 degrees. since triangle ABC is an equilateral triangle, then we can deduce that angle ABC is 60 degrees which meant angle EFG is also 60 degrees. by using 30-60-90 rule or sin/cos/tan, we can find out the sides of EF which is 3 plus 3/root 3. and then using 30-60-90 rule or cos 60, we can find FG. my previous post have more detail formulas. thanks!
Angles ABC, EFG are 60 degrees. The next step does not make any sense. the 30-60-90 rule tells us about ratios of the sides. How do you get the length of EF from ratios? Of course, you need to prove that angle FEG is 90 degrees to even use the 30-60-90 rule.
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 618
Beer soaked ramblings follow.
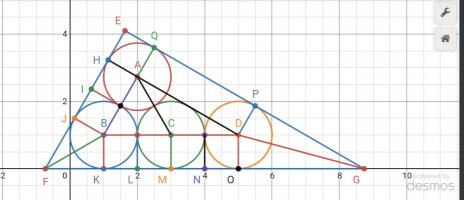
A somewhat better description might be:
J to E is equal to 3.
Since angle EFG is 60, it follows that angle JFB & angle BFK is 1/2 of 60 or 30.
KB is 1 and is opposite a the 30 degree angle; thus, hypotenuse FB must be 2 since in a right triangle having acute angles 30° & 60°, the length of the side opposite the 30° is 1/2 the length of the hypotenuse. We then have
[imath]FK=FJ=\sqrt{2^2-1^2}=\sqrt{3}[/imath]
and
[imath]FG=JE+FJ=3+\sqrt{3}[/imath].
... side EF = 3 + 3/root 3 ...
... by using 30-60-90 rule or sin/cos/tan, we can find out the sides of EF which is 3 plus 3/root 3. ...

A somewhat better description might be:
J to E is equal to 3.
Since angle EFG is 60, it follows that angle JFB & angle BFK is 1/2 of 60 or 30.
KB is 1 and is opposite a the 30 degree angle; thus, hypotenuse FB must be 2 since in a right triangle having acute angles 30° & 60°, the length of the side opposite the 30° is 1/2 the length of the hypotenuse. We then have
[imath]FK=FJ=\sqrt{2^2-1^2}=\sqrt{3}[/imath]
and
[imath]FG=JE+FJ=3+\sqrt{3}[/imath].
Last edited:
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,852
Although the problem doesn't require a formal proof, it is necessary at least to convince yourself that angle E measures 90 degrees; the OP said "we can deduce that angle E is 90 degrees" without stating the reasoning.Sorry, you can't assume that the angle E is 90 degrees based on the diagram. If it's not given that it's 90, then don't assume that it's 90.
One way to see it is to observe that the sides of EFG are parallel to those of ABD, so they are similar; and that A, B, and D lie on a circle of radius 2 centered at C, so that angle BAD is a right angle. Then it follows that ABD, and therefore EFG, is a 30-60-90 triangle, and FG is twice EG, which is easily calculated as we've seen, given that E is a right angle and JBF is 30-60-90.
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
But OP did state the reasoning: "since the shape of the vertex E is a square, we can deduce that angle E is 90 degrees"Although the problem doesn't require a formal proof, it is necessary at least to convince yourself that angle E measures 90 degrees; the OP said "we can deduce that angle E is 90 degrees" without stating the reasoning.
One way to see it is to observe that the sides of EFG are parallel to those of ABD, so they are similar; and that A, B, and D lie on a circle of radius 2 centered at C, so that angle BAD is a right angle. Then it follows that ABD, and therefore EFG, is a 30-60-90 triangle, and FG is twice EG, which is easily calculated as we've seen, given that E is a right angle and JBF is 30-60-90.
I assumed this meant "The angle looks like it's 90 degrees, so we'll go with that". Of course, my assumption may be wrong too. If someone has a different interpretation of "the shape of the vertex E is a square", I'd like to hear it.
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 618
Beer induced reaction follows.
Didn't see that one.... and that A, B, and D lie on a circle of radius 2 centered at C, so that angle BAD is a right angle. ...

