Matthewhistorian
New member
- Joined
- Nov 11, 2021
- Messages
- 5
For a question like this 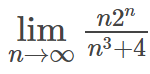 , I know how to solve the limit normally but I was wondering if a possible way of solving it would be to break it up into n/1 multiplied by (2^n)/(n^3+4) and since both functions are a faster growing function over a slower function the end result is still infinity. If that doesn't work can anyone explain why and if there's any examples where you can't just multiply two fast/slow functions to get a fast/slow function?
, I know how to solve the limit normally but I was wondering if a possible way of solving it would be to break it up into n/1 multiplied by (2^n)/(n^3+4) and since both functions are a faster growing function over a slower function the end result is still infinity. If that doesn't work can anyone explain why and if there's any examples where you can't just multiply two fast/slow functions to get a fast/slow function?
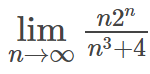 , I know how to solve the limit normally but I was wondering if a possible way of solving it would be to break it up into n/1 multiplied by (2^n)/(n^3+4) and since both functions are a faster growing function over a slower function the end result is still infinity. If that doesn't work can anyone explain why and if there's any examples where you can't just multiply two fast/slow functions to get a fast/slow function?
, I know how to solve the limit normally but I was wondering if a possible way of solving it would be to break it up into n/1 multiplied by (2^n)/(n^3+4) and since both functions are a faster growing function over a slower function the end result is still infinity. If that doesn't work can anyone explain why and if there's any examples where you can't just multiply two fast/slow functions to get a fast/slow function?