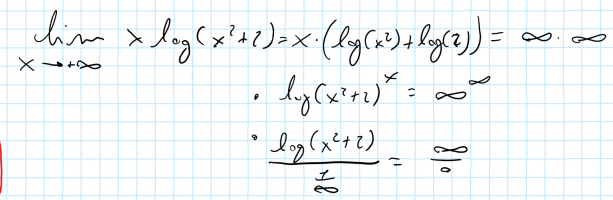You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How do you calculate this limit?
- Thread starter itsrayex
- Start date
What does your text list as indeterminate forms?
[math]x > e \implies x^2 + 2 > e \implies ln(x^2 + 2) > 1.\\ \therefore x > e > 0 \implies x * ln(x^2 + 2) > x * 1 = x.[/math]
Now apply the formal definitions of the limit as x approaches infinity and the limit equals infinity.
I point out that [imath]log(x^2 + 2) \ne log(x^2) + log(2) = log(2x^2).[/imath]
[math]x > e \implies x^2 + 2 > e \implies ln(x^2 + 2) > 1.\\ \therefore x > e > 0 \implies x * ln(x^2 + 2) > x * 1 = x.[/math]
Now apply the formal definitions of the limit as x approaches infinity and the limit equals infinity.
I point out that [imath]log(x^2 + 2) \ne log(x^2) + log(2) = log(2x^2).[/imath]
Last edited:
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
[math]\lim_{x\to \infty}x\log(x^2+2)=(\lim_{x\to \infty}x)(\lim_{x\to \infty}\log(x^2+2))=\infty\cdot\infty=\infty[/math]
Turns out I mistakenly thought infinite*infinite is an indeterminate form, but it's not. Thank you!What does your text list as indeterminate forms?
[math]x > e \implies x^2 + 2 > e \implies ln(x^2 + 2) > 1.\\ \therefore x > e > 0 \implies x * ln(x^2 + 2) > x * 1 = x.[/math]
Now apply the formal definitions of the limit as x approaches infinity and the limit equals infinity.
I point out that [imath]log(x^2 + 2) \ne log(x^2) + log(2) = log(2x^2).[/imath]