Hello everyone.

I'm trying to solve this exercise, but I'm having the following problems:
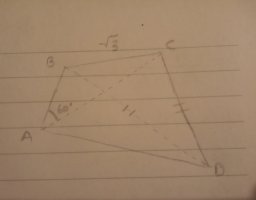
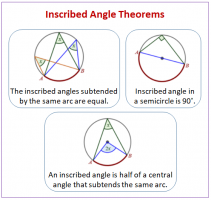
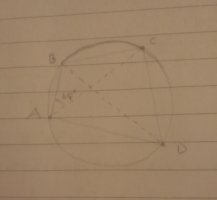
-I saw a video where it was said that since BAC = 60°, then BDC = 60° too, but I don't understand why.
-I also easily get confused with the graph, I tried to draw a quadrangle accurately according to the information given (and it took me too long I think), but in the video I mentioned it seems that they drew the same thing but upside-down, and I know the graph should only be used as a reference but all the lines and lengths end up confusing me.
-Then, I don't know how to find the circumradius. Do I need to know a formula? In the video they find the circumradius of the triangle BCD, which is 1, and then say that it is the correct result for 1). But in the exercise they are asking for the circumradius of the quadrangle ABCD, not the triangle BCD. I'm also a bit lost here.
If I manage to understand 1), I think I could do 2) without major difficulties.
Any help would be much appreciated.

I'm trying to solve this exercise, but I'm having the following problems:
-I saw a video where it was said that since BAC = 60°, then BDC = 60° too, but I don't understand why.
-I also easily get confused with the graph, I tried to draw a quadrangle accurately according to the information given (and it took me too long I think), but in the video I mentioned it seems that they drew the same thing but upside-down, and I know the graph should only be used as a reference but all the lines and lengths end up confusing me.
-Then, I don't know how to find the circumradius. Do I need to know a formula? In the video they find the circumradius of the triangle BCD, which is 1, and then say that it is the correct result for 1). But in the exercise they are asking for the circumradius of the quadrangle ABCD, not the triangle BCD. I'm also a bit lost here.
If I manage to understand 1), I think I could do 2) without major difficulties.
Any help would be much appreciated.
Last edited by a moderator:


![CENTER]](https://i.ibb.co/kGqhDJ4/Exact-Values.png[/img[/FONT][/SIZE][/CENTER])