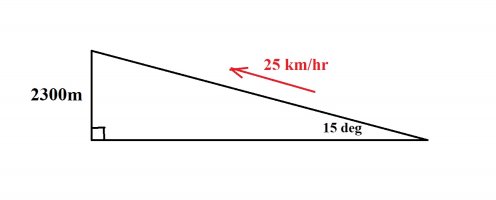
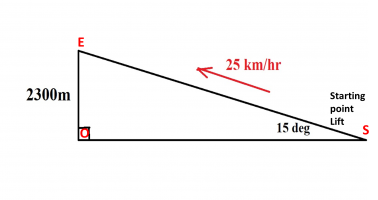
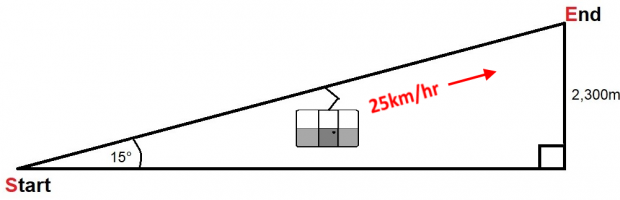
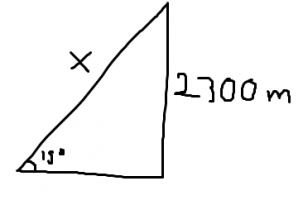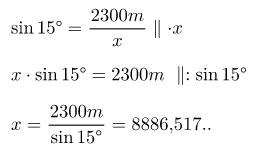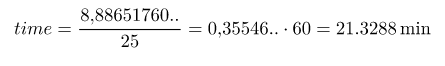The landscape lift travels at an angle of 15 degrees at a speed of 25 km/h. The height difference between the departure point and the elevator ending point is 2300m. How long does it take the elevator to travel? Give the answer to the nearest minute.
The only answer I got was 5 minutes, but I did not include the 15 degrees. I managed to calculate the time using only speed and distance. I have no idea how to include the 15 degrees with it.
The only answer I got was 5 minutes, but I did not include the 15 degrees. I managed to calculate the time using only speed and distance. I have no idea how to include the 15 degrees with it.
Last edited: