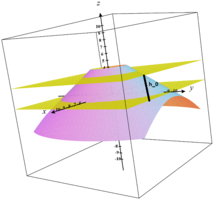
This question may be simple, but I could not calculate in principle and accurately.
The equation of the cone is [imath]z=\sqrt{\frac{x^2}{a^2}+\frac{y^2}{b^2}}[/imath]. My goal is to calculate a part of the surface of the cone, which is located between two planes [imath]z=z_0[/imath] and [imath]z=z_1 > z_0[/imath] so that the interface between plane [imath]z=z_0[/imath] and cone is an ellipse with large radius a and small radius b and the distance between the top plane and the bottom plane is [imath]h_0[/imath].
The equation of the cone is [imath]z=\sqrt{\frac{x^2}{a^2}+\frac{y^2}{b^2}}[/imath]. My goal is to calculate a part of the surface of the cone, which is located between two planes [imath]z=z_0[/imath] and [imath]z=z_1 > z_0[/imath] so that the interface between plane [imath]z=z_0[/imath] and cone is an ellipse with large radius a and small radius b and the distance between the top plane and the bottom plane is [imath]h_0[/imath].