You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How would I go about approaching this question?
- Thread starter pope4
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
Please show the data you wrote down, so we can be sure you found everything you need.I tried doing this question over and over again and I can't even begin to imagine how to solve it. I wrote down the available data (x-intercepts, constant term, even or
odd exponent) and I'm still not sure how to do it. Thank you for the help!
View attachment 34297
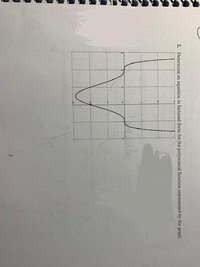
Here's the graph:
One thing you need is the x-intercepts. What are they?
Another is the multiplicities of the x-intercepts. What do you think they might be?
With those, you can make your first attempt at a polynomial, in factored form. What will that be?
Then there may be some adjustments needed (to get the right y-intercept), but that can wait.
I wrote down that the x-intercepts are 1 and -2, both with multiplicities of 3, that the y-intercept is -2, therefore the constant term is -2, and that the exponent has to be positive. This led me to f(x)=a(x-1)^3(x+2)^3, but needless to say this did lead me towards a sensible solution.Please show the data you wrote down, so we can be sure you found everything you need.
Here's the graph:
One thing you need is the x-intercepts. What are they?
Another is the multiplicities of the x-intercepts. What do you think they might be?
With those, you can make your first attempt at a polynomial, in factored form. What will that be?
Then there may be some adjustments needed (to get the right y-intercept), but that can wait.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
I take it you did determine a, and solve the problem? The word "but" could suggest otherwise.I wrote down that the x-intercepts are 1 and -2, both with multiplicities of 3, that the y-intercept is -2, therefore the constant term is -2, and that the exponent has to be positive. This led me to f(x)=a(x-1)^3(x+2)^3, but needless to say this did lead me towards a sensible solution.
It may be worth noting that in factored form, there is no "constant term"; that's the y-intercept, which you use to find a by determining f(0).
I'm not sure what you mean by "the exponent has to be positive". There are no negative exponents in a polynomial. Maybe you meant even.
Sorry I made a bunch of grammar mistakes in that sentence! I didn't end up finding a solution, and 'even exponent' is what I meant to say (English isn't my first language and despite quite a bit of experience I have with it I still keep mistaking 'even' and 'odd' for 'positive' and 'negative', quite a troublesome trait to have).I take it you did determine a, and solve the problem? The word "but" could suggest otherwise.
It may be worth noting that in factored form, there is no "constant term"; that's the y-intercept, which you use to find a by determining f(0).
I'm not sure what you mean by "the exponent has to be positive". There are no negative exponents in a polynomial. Maybe you meant even.
I wasn't sure if I was doing it right by writing down the factored solution I mentioned earlier since, after expanding it, I got some obscene equation (x^6+3x^5-3x^4-11x^3+6x^2+12x-8). However, assuming the equation was somehow correct, how would I go about finding a?
blamocur
Elite Member
- Joined
- Oct 30, 2021
- Messages
- 3,222
You've done a good job! All that remains is finding 'a' : what is the value of f(0) ?Sorry I made a bunch of grammar mistakes in that sentence! I didn't end up finding a solution, and 'even exponent' is what I meant to say (English isn't my first language and despite quite a bit of experience I have with it I still keep mistaking 'even' and 'odd' for 'positive' and 'negative', quite a troublesome trait to have).
I wasn't sure if I was doing it right by writing down the factored solution I mentioned earlier since, after expanding it, I got some obscene equation (x^6+3x^5-3x^4-11x^3+6x^2+12x-8). However, assuming the equation was somehow correct, how would I go about finding a?
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,596
I am sorry but 3 is not even. What did you mean by an even exponent?I wrote down that the x-intercepts are 1 and -2, both with multiplicities of 3, that the y-intercept is -2, therefore the constant term is -2, and that the exponent has to be even. This led me to f(x)=a(x-1)^3(x+2)^3, but needless to say this did lead me towards a sensible solution.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
I occasionally do that myself, in a context where both ideas occur (such as even powers of negative numbers).I still keep mistaking 'even' and 'odd' for 'positive' and 'negative', quite a troublesome trait to have
You were told to keep it in factored form, for a reason. That's the natural form for this sort of problem.I wasn't sure if I was doing it right by writing down the factored solution I mentioned earlier since, after expanding it, I got some obscene equation (x^6+3x^5-3x^4-11x^3+6x^2+12x-8). However, assuming the equation was somehow correct, how would I go about finding a?
You know that f(x) = a(x-1)^3(x+2)^3, and that f(0) = -2. Put those together: a(0-1)^3(0+2)^3 = -2, and solve for a. You were so close I assumed you had taken this last step. As I'd said, "Then there may be some adjustments needed (to get the right y-intercept), but that can wait."
That refers to the total power: This is a 6th degree equation; you can see it's even because it rises at both ends. Surely you can see that?I am sorry but 3 is not even. What did you mean by an even exponent?