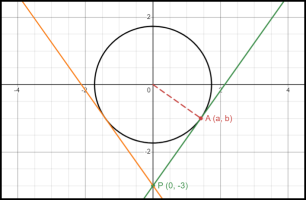
circle O is determined by the equation x^2 + y^2 = 3.
Point P has coordinates (0, -3)
Let A with coordinates (a, b), be a point on circle O so that AP is tangent to the circle.
Point P has coordinates (0, -3)
Let A with coordinates (a, b), be a point on circle O so that AP is tangent to the circle.
- Find coordinates (a, b) for such a point A.
- Remember to notate your work and indicate how you are applying any relevant definitions or theorems.