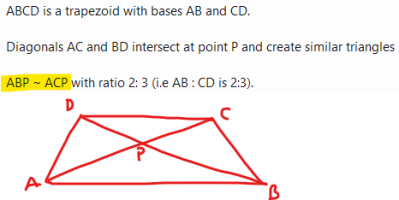
ABCD is a trapezoid with bases AB and CD.
Diagonals AC and BD intersect at point P and create similar triangles
АВР ~ ACP with ratio 2: 3 (i.e AB : CD is 2:3).
Point A is at (-6, -8), point C is at (9, 12), and point B is in quadrant II.
Find the intersection point P of the diagonals.
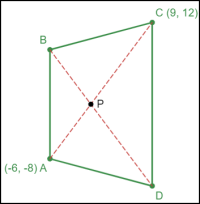
Diagonals AC and BD intersect at point P and create similar triangles
АВР ~ ACP with ratio 2: 3 (i.e AB : CD is 2:3).
Point A is at (-6, -8), point C is at (9, 12), and point B is in quadrant II.
Find the intersection point P of the diagonals.