jamestrickington
New member
- Joined
- Jan 7, 2024
- Messages
- 6
I have a question from Measure Theory / Probability Theory. This is the question:
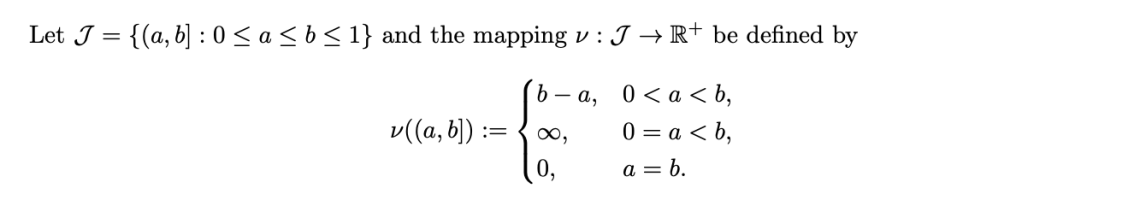
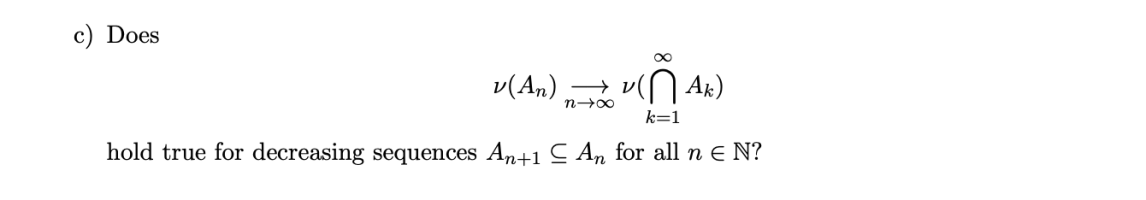
I have established that the measure v is not sigma-additive.
I have also checked the value of An for most cases.
I am only interested in the case where An = (0, bn] where as n -> inf, b -> 0. In this case, does the infinite countable intersection of An become the empty set? If so then the statement does not hold.
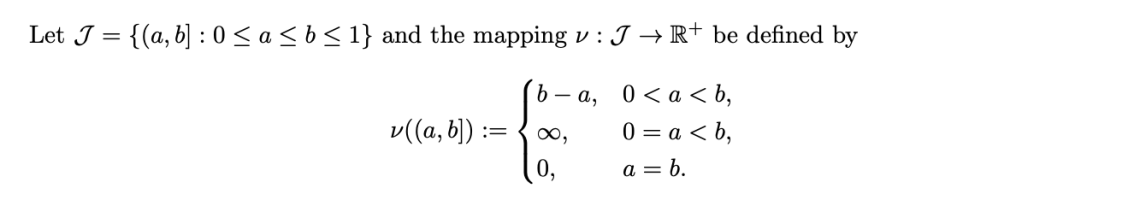
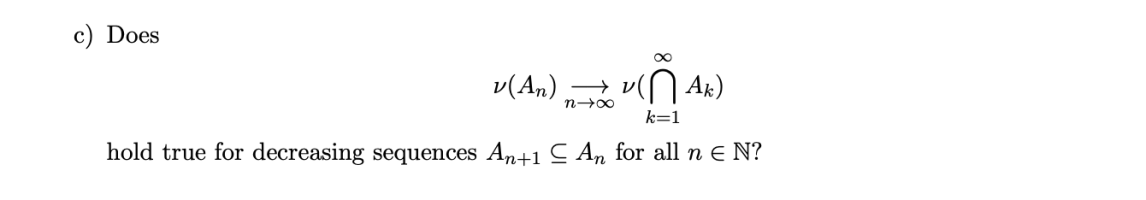
I have established that the measure v is not sigma-additive.
I have also checked the value of An for most cases.
I am only interested in the case where An = (0, bn] where as n -> inf, b -> 0. In this case, does the infinite countable intersection of An become the empty set? If so then the statement does not hold.

