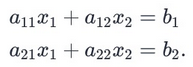You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Conisder the (2X2) system
- Thread starter Integrate
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
When I don't know what to do, I sometimes try playing with the problem using specific numbers. Pick some numbers for the a's and b's, and try doing what they ask. That may give you ideas for what to do in general.View attachment 39050
I understand I am supposed to show work with this but I am really lost on how to start. Can I get a nudge in the right direction on how to start?
Thank you
It may also help if you tell us what you have been learning recently, since that may suggest what we should or shouldn't expect of you.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
Okay; I suppose you haven't been introduced to matrices yet, or to specific things to do with them; I wouldn't expect you to be using those ideas anyway.
Please try what I suggested. If, say, the given equations were 2x + 3y = 4 and 3x + 1y = 2, where (2)(1) - (3)(3) = -7 which is not 0, how would you eliminate the coefficient of x in the second equation? And what would you do differently if the first 2 were replaced with 0?
Then do the same things with unspecified parameters, as given.
The more though you show, the easier it will be to help you.
Please try what I suggested. If, say, the given equations were 2x + 3y = 4 and 3x + 1y = 2, where (2)(1) - (3)(3) = -7 which is not 0, how would you eliminate the coefficient of x in the second equation? And what would you do differently if the first 2 were replaced with 0?
Then do the same things with unspecified parameters, as given.
The more though you show, the easier it will be to help you.
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
As an expert in differential equations and matrices, I would suggest to move the first system to a Matrix notation. Then you can easily show that system \(\displaystyle 1 \equiv \) system \(\displaystyle 2\) by using Matrix properties.View attachment 39050
I understand I am supposed to show work with this but I am really lost on how to start. Can I get a nudge in the right direction on how to start?
Thank you
Integrate
Junior Member
- Joined
- May 17, 2018
- Messages
- 129
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
First, is there a reason you used AI or someone else to solve this, rather than follow our suggestions to try it yourself, and show us your thoughts? This is a very bad way to learn anything. (Especially when the sources you rely on are full of errors.)
Second, have you actually already learned about matrices and row reduction, as your initial response appeared to deny, since I wouldn't expect the very first section to go that far? That makes a big difference.
As for the actual proof, it's full of errors. The first one I saw was the last bit of Step 1, where they have gone back to the original system rather than show the result of what they said they were about to do!
But there's more. You have to read every step and correct it. (Or just ignore the whole thing!)
I was going to list errors, but there are too many to describe. This is really horrible!
You don't have to believe that everyone except you is right. If you see something wrong, do the right thing instead.
Go back to the start, and try solving the problem yourself. Clearly you are not finding good help, wherever that comes from. But whatever you try doing yourself, you'll at least know what you really did, and we can talk about it.
Second, have you actually already learned about matrices and row reduction, as your initial response appeared to deny, since I wouldn't expect the very first section to go that far? That makes a big difference.
As for the actual proof, it's full of errors. The first one I saw was the last bit of Step 1, where they have gone back to the original system rather than show the result of what they said they were about to do!
But there's more. You have to read every step and correct it. (Or just ignore the whole thing!)
Because that's what the problem says to do. When you have some valid work, you might want to see what it would look like if a11 were zero. In fact, you should -- that's the only way to learn.First off, why do we differentiate between when a11 is zero and non-zero?
Clearly that's not really what they did. So figure out what they meant, and do that.And why does the solution go R_2-a11R_1 -> R2
I was going to list errors, but there are too many to describe. This is really horrible!
There are different ways to do elimination.Why does it [not?] follow general gaussian elimination order? Shouldn't we be trying to make a11 a entry of 1?
So fix their error! What do you need to do instead?If we multiply row 1 by a21/a11 and add to row 2 we should get
You don't have to believe that everyone except you is right. If you see something wrong, do the right thing instead.
Go back to the start, and try solving the problem yourself. Clearly you are not finding good help, wherever that comes from. But whatever you try doing yourself, you'll at least know what you really did, and we can talk about it.
Integrate
Junior Member
- Joined
- May 17, 2018
- Messages
- 129
I have been for the entirety of this and you're right I should have posted my work. A lot could have been gleaned from it. I also just seem to not understand forums and am reluctant to use latex, but I am improving.try it yourself
Here is the question written in latex
Consider the [imath](2\times2)[/imath] system
[math]a_{11}x_{1}+a_{12}x_{2}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}=b_{2}[/math]Show that if [imath]a_{11}a_{22}-a_{12}a_{21}\neq0[/imath], then this system
is equivalent to a system of the form
[math]c_{11}x_1+c_{12}x_2=d_1[/math][math]c_{22}x_2=d_2,[/math]where [imath]c_{11}\neq0[/imath] and [imath]c_{22}\neq0.[/imath] Note that the second
system always has a solution. [Hint: First suppose that [imath]a_{11}\neq0[/imath], and then consider the special case in which [imath]a_{11}=0[/imath].]
Here is my work.
1.) I create an augmented matrix of the first system
[math]\begin{bmatrix} a_{11} & a_{12} & b_{1}\\ a_{21} & a_{22} & b_{2}\\ \end{bmatrix}[/math]
2. ) I have been learning how to do Gauss-Jordan Elimination, so I assume that is what I am to do and do as such.
I assume [imath]a_{11}[/imath]is not zero, and I want to get [imath]a_{11}[/imath] via Gauss-Jordan method, so I use the following elementary row operations to do such.
[math]\frac{R_{1}}{a_{11}} \longrightarrow R_{1}[/math]
Which gives us
[math]\begin{bmatrix} 1 & \frac{a_{12}}{a_{11}} & \frac{b_1}{a_{11}}\\ a_{21} & a_{22} & b_2 \end{bmatrix}[/math]
2.) Now that we have 1 for the [imath]a_{11}[/imath] entry I want to put zero in the rest of its column and I use the elementary row operations to do such.
[math]R_{2} - a_{11}*R_{1}\longrightarrow R_{2}[/math]
Which gives us
[math]\begin{bmatrix} 1 & \frac{a_{12}}{a_{11}} & \frac{b_1}{a_{11}}\\ 0 & a_{22}-\frac{a_{12}a_{21}}{a_{11}} & b_2 - \frac{b_1a_{21}}{a_{11}} \end{bmatrix}[/math]
3.) I recognize some familiar algebra in the [imath]a_{22}[/imath] entry [math]a_{22}-\frac{a_{12}a_{21}}{a_{11}}[/math] and with algebraic manipulation rearrange it to this [math]\frac{a_{11}a_{22}-a_{12}a_{21}}{a_{11}}[/math]
Which the problem tells us to assume that [math]a_{11}a_{22}-a_{12}a_{21} \not= 0[/math]
4.) Okay, so we finally got to a point in the problem where the prompt seems familiar enough to lets us know we are on the right track. That we have our first system of linear equation modified enough that we can start making an analysis of row equivalence within the constraints of the prompt.
5.) I create an augmented matrix for the second set of linear equations
[math]\begin{bmatrix} c_{11} & c_{12} & d_{1} \\ c_{21} & c_{22} & d_{2} \\ \end{bmatrix}[/math]
6.) I remember that I am told to assume that [imath]c_{11}\neq0[/imath] and [imath]c_{22}\neq0.[/imath], I and remember that [imath]a_{11}a_{22}-a_{12}a_{21} \not= 0[/imath], and we made our own assumption via hint that [imath]a_{11} \not=[/imath]. Meaning that all of these do not equal zero. So with all of that in mind and the fact we were able to use elementary row operations, we have hopefully shown that both systems are row equivalent when making these assumptions.
Edit: I forgot to convert a row back in this where it would return it to the original augmented form. I'm aware I didn't but it doesn't change the rest of the steps.
Last edited:
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
You have been ... what? Did you leave out a word? And are you confirming that the section you've read in the book covers matrices? The problem can be solved without them.I have been for the entirety of this and you're right I should have posted my work. A lot could have been gleaned from it. I also just seem to not understand forums and am reluctant to use latex, but I am improving.
You don't need to use LaTeX here unless you want to.
I made your correction.1.) I create an augmented matrix of the first system
[math]\begin{bmatrix} a_{11} & a_{12} & b_{1}\\ a_{21} & a_{22} & b_{2}\\ \end{bmatrix}[/math]
2. ) I have been learning how to do Gauss-Jordan Elimination, so I assume that is what I am to do and do as such.
I assume [imath]a_{11}[/imath]is not zero, and I want to get [imath]a_{11}[/imath] via Gauss-Jordan method, so I use the following elementary row operations to do such.
[math]\frac{R_{1}}{a_{11}} \longrightarrow R_{1}[/math]
Which gives us
[math]\begin{bmatrix} 1 & \frac{a_{12}}{a_{11}} & \frac{b_1}{a_{11}}\\ a_{21} & a_{22} & b_2 \end{bmatrix}[/math]
2.) Now that we have 1 for the [imath]a_{11}[/imath] entry I want to put zero in the rest of its column and I use the elementary row operations to do such.
[math]R_{2} - a_{21}*R_{1}\longrightarrow R_{2}[/math]
Which gives us
[math]\begin{bmatrix} 1 & \frac{a_{12}}{a_{11}} & \frac{b_1}{a_{11}}\\ 0 & a_{22}-\frac{a_{12}a_{21}}{a_{11}} & b_2 - \frac{b_1a_{21}}{a_{11}} \end{bmatrix}[/math]
Do you see why that assumption was required? And, more important, why in this part of the work you have to assume a11 is not zero, and have to do a second part if it is?3.) I recognize some familiar algebra in the [imath]a_{22}[/imath] entry [math]a_{22}-\frac{a_{12}a_{21}}{a_{11}}[/math] and with algebraic manipulation rearrange it to this [math]\frac{a_{11}a_{22}-a_{12}a_{21}}{a_{11}}[/math]
Which the problem tells us to assume that [math]a_{11}a_{22}-a_{12}a_{21} \not= 0[/math]
I don't think you need to do this. Just look at the augmented matrix you got to, and write it as a system of equations. Compare to the requires form; do you see that it is in that form? What are c11, etc?4.) Okay, so we finally got to a point in the problem where the prompt seems familiar enough to lets us know we are on the right track. That we have our first system of linear equation modified enough that we can start making an analysis of row equivalence within the constraints of the prompt.
5.) I create an augmented matrix for the second set of linear equations
[math]\begin{bmatrix} c_{11} & c_{12} & d_{1} \\ c_{21} & c_{22} & d_{2} \\ \end{bmatrix}[/math]
No, you aren't told to assume that; you are to show that when you write the system in this form, that will be true. The new coefficients don't exist until you name them!6.) I remember that I am told to assume that [imath]c_{11}\neq0[/imath] and [imath]c_{22}\neq0.[/imath], I and remember that [imath]a_{11}a_{22}-a_{12}a_{21} \not= 0[/imath], and we made our own assumption via hint that [imath]a_{11} \not=[/imath]. Meaning that all of these do not equal zero. So with all of that in mind and the fact we were able to use elementary row operations, we have hopefully shown that both systems are row equivalent when making these assumptions.
I'm not sure what you are referring to.Edit: I forgot to convert a row back in this where it would return it to the original augmented form. I'm aware I didn't but it doesn't change the rest of the steps.
Integrate
Junior Member
- Joined
- May 17, 2018
- Messages
- 129