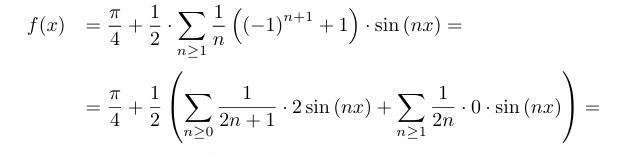Fourier Series exercise

[wolly]

How does the first line equal the second line?This is a Fourier Series!
Where do 0 and [math]\frac{1}{2n+1}[/math] appear from?

 

[blamocur]

What are the values of [imath](-1)^{n+1}+1[/imath] for odd and even [imath]n[/imath]'s ?

 

[wolly]

What are the values of [imath](-1)^{n+1}+1[/imath] for odd and even [imath]n[/imath]'s ?

For [math]n=0=>0[/math][math]n=1=>2[/math][math]n=2=>0[/math][math]n=3=>2[/math]So the values are 0 and 2!

 

[logistic_guy]

View attachment 39343
How does the first line equal the second line?This is a Fourier Series!
Where do 0 and [math]\frac{1}{2n+1}[/math] appear from?

The idea is that we want to sum only when \(\displaystyle n\) is odd

Then,

\(\displaystyle \frac{(-1)^{n+1} + 1}{n} = \frac{2}{2n + 1}\)

We start in the first with \(\displaystyle n = 1\) while we start in the second with \(\displaystyle n = 0\).

But your book is wrong!

\(\displaystyle \sum_{n=1}\frac{(-1)^{n+1} + 1}{n}\sin nx \neq \sum_{n=0}\frac{2}{2n + 1}\sin nx\)

It should be:

\(\displaystyle \sum_{n=1}\frac{(-1)^{n+1} + 1}{n}\sin nx = \sum_{n=0}\frac{2}{2n + 1}\sin (2n + 1)x\)


Do you see the difference and why?

 

[wolly]

The idea is that we want to sum only when \(\displaystyle n\) is odd

Then,

\(\displaystyle \frac{(-1)^{n+1} + 1}{n} = \frac{2}{2n + 1}\)

We start in the first with \(\displaystyle n = 1\) while we start in the second with \(\displaystyle n = 0\).

But your book is wrong!

\(\displaystyle \sum_{n=1}\frac{(-1)^{n+1} + 1}{n}\sin nx \neq \sum_{n=0}\frac{2}{2n + 1}\sin nx\)

It should be:

\(\displaystyle \sum_{n=1}\frac{(-1)^{n+1} + 1}{n}\sin nx = \sum_{n=0}\frac{2}{2n + 1}\sin (2n + 1)x\)


Do you see the difference and why?

Can you show me how you got the [math]\frac{2}{2n+1}*sin(2n+1)x[/math]?

 

[logistic_guy]

Can you show me how you got the [math]\frac{2}{2n+1}*sin(2n+1)x[/math]?

In your post #3 you have shown that only the odd index of summation matters, ie \(\displaystyle n = 1,3,5,7....\)

The trick is that if we want only even indices we change \(\displaystyle n\) to \(\displaystyle 2n\)

And

If we want only odd indices we change \(\displaystyle n\) to \(\displaystyle 2n + 1\)

Why?

Because \(\displaystyle 2n + 1\) allows us to get the odd indices again. Here are some calculations:

\(\displaystyle 2(0) + 1 = 1\)
\(\displaystyle 2(1) + 1 = 3\)
\(\displaystyle 2(2) + 1 = 5\)
\(\displaystyle 2(3) + 1 = 7\)

Aren't these the same as \(\displaystyle n = 1,3,5,7....\)?

The second part is that if we change one \(\displaystyle n\) to \(\displaystyle 2n + 1\), we have to change all other \(\displaystyle n\)'s to \(\displaystyle 2n + 1\).

In the original summation, we have:

\(\displaystyle \sum_{n=1}\frac{(-1)^{n+1} + 1}{n}\sin nx\)

It means that we have two \(\displaystyle n\)'s. So we have to change them both. And we get:

\(\displaystyle \sum_{n=0}\frac{2}{2n + 1}\sin (2n + 1)x\)

And because we care only for the odd \(\displaystyle n\), \(\displaystyle (-1)^{n+1} + 1\) is always \(\displaystyle = 2\)

 

[logistic_guy]

temperature in a hemisphere

The steady-state temperature in a hemisphere of radius r = c is determined from \frac{\partial^2 u}{\partial r^2} + \frac{2}{r}\frac{\partial u}{\partial r} + \frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2} + \frac{\cot \theta}{r^2}\frac{\partial u}{\partial \theta} = 0 0 < r < c, \ \ \ \...

www.freemathhelp.com

See post #6. The idea of the odd index \(\displaystyle 2n + 1\) was used there.