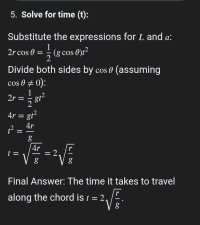logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
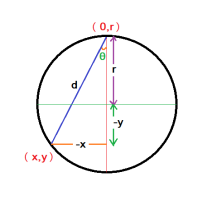
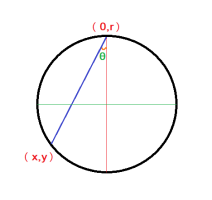
An object is placed at the top of a vertical circle whose equation is \(\displaystyle x^2 + y^2 = r^2\). Assuming gravity is the only force acting on the object, how long does it take to travel along a chord to the point \(\displaystyle (x,y)\) on the circle? A chord is drawn from the top of the circle to \(\displaystyle (x,y)\) to represent the path of the object.
Does the object reach \(\displaystyle (x,y)\) faster via a shorter or longer chord? Explain your reasoning.
I couldn’t solve this problem. Would you have failed too?


Interestingly, this problem was given to elementary school students in \(\displaystyle \text{China}\) and surprisingly \(\displaystyle 99\%\) of them solved it correctly. When the same problem was presented to college students around the world, only a small number managed to answer it.
If I, the self-proclaimed Lord of Mathematics, couldn't crack it, then surely it is understandable if you would struggle with it too!
The correct answer will be revealed after seeing some attempts! If you decide to take on this challenge, please don’t resort to cheating. Thank you.
Does the object reach \(\displaystyle (x,y)\) faster via a shorter or longer chord? Explain your reasoning.

I couldn’t solve this problem. Would you have failed too?
Interestingly, this problem was given to elementary school students in \(\displaystyle \text{China}\) and surprisingly \(\displaystyle 99\%\) of them solved it correctly. When the same problem was presented to college students around the world, only a small number managed to answer it.
If I, the self-proclaimed Lord of Mathematics, couldn't crack it, then surely it is understandable if you would struggle with it too!
The correct answer will be revealed after seeing some attempts! If you decide to take on this challenge, please don’t resort to cheating. Thank you.
Last edited: