logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
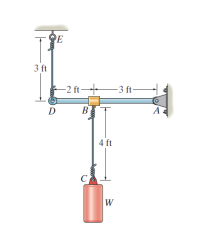
The bar \(\displaystyle DA\) is rigid and originally held in the horizontal position when the weight \(\displaystyle W\) is supported from \(\displaystyle C\). If the weight causes \(\displaystyle B\) to be displaced downward \(\displaystyle 0.025 \ \text{in}\), determine the strain in wires \(\displaystyle DE\) and \(\displaystyle BC\). Also, if the wires are made of \(\displaystyle \text{A-36}\) steel and have a cross-sectional area of \(\displaystyle 0.002 \ \text{in}^2\), determine the weight \(\displaystyle W\).