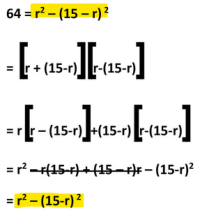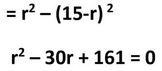You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculate the QM and the radius
- Thread starter chijioke
- Start date
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
Have you heard of the formula: Circumradius formula.b. calculate the radius of the circle to the nearest whole number.
\(\displaystyle r = \frac{abc}{4A}\)
where \(\displaystyle a,b,c\) are the side lengths of the triangle and \(\displaystyle A\) is the triangle area.
Or
\(\displaystyle r = \frac{a}{2\sin A}\), where \(\displaystyle a = \overline{PR}\) and \(\displaystyle A\) the angle opposite to it.
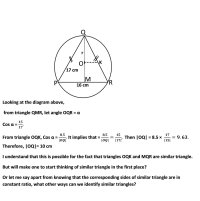
The formula gives the radius of the circle for any triangle inscribed inside when all vertices of the triangle touch the circumference of the circle.
If you are not allowed to use this formula and you want to solve the problem using pure geometry, you can construct the perpendicular bisectors.
Last edited:
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
I think there's a typo there:
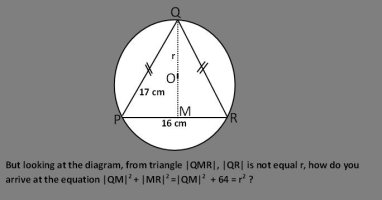
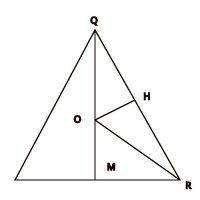
In particular, OM = 15 - r.I'd use these facts:
but this is not the only approach.
- QO = OR = r
- QO + OM = QM = 15
- OM^2 + MR^2 = OM^2 + 64 = r^2
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 618
Beer drenched reaction follows.
You're clearly suffering from some kind amnesia.
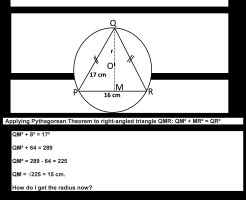
An isosceles triangle PQR has it vertices on the circumference of a circle. If |PQ| = |QR| = 17 cm, |PR| = 16 cm and m is the midpoint of |PR|. Calculate
a. |QM|
b. calculate the radius of the circle to the nearest whole number.
View attachment 39607
You're clearly suffering from some kind amnesia.
How do I find the radius of the circle? (An isosceles triangle ABC has its vertices on a circle....)
i. Let the height \overline{BM}~\text{be x} x=\sqrt{13^2-5^2}=12 cm \therefore the height of the triangle \overline{BM}=12cm ii. So how can I obtain the radius of the circle?
www.freemathhelp.com
Last edited:
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
Relax man! It is very normal that people forget how to solve the same problem twice after some time passes. I myself who is considered the greatest Lord of mathematics in the history of this forum, I forget how to solve the same problem after one week from the solution. Now imagine this @chijioke who did it last time two years ago!You're clearly suffering from some kind amnesia.
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 618
Beer drenched non sequitur ramblings follow.
Spider marriage is complicated. Sometimes, you just gotta mind your own biz.
Relax ...
Spider marriage is complicated. Sometimes, you just gotta mind your own biz.
logistic_guy: I myself who is considered the greatest Lard of mathematics in the history of this forum.
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
@lookagainlogistic_guy: I myself who is considered the greatest Lard of mathematics in the history of this forum.
What ever you say about me, I still love you man!
If I mind only my own biz, where is the fun in that?Spider marriage is complicated. Sometimes, you just gotta mind your own biz.
jonah2.0
Full Member
- Joined
- Apr 29, 2014
- Messages
- 618
Beer drenched non sequitur ramblings follow.
Cockroach community dynamics is complicated. They eat their dead so that nothing goes to waste. It's best to stay out of their biz.
...
If I mind only my own biz, where is the fun in that? ...
Cockroach community dynamics is complicated. They eat their dead so that nothing goes to waste. It's best to stay out of their biz.
Have you heard of the formula: Circumradius formula.
\(\displaystyle r = \frac{abc}{4A}\)
where \(\displaystyle a,b,c\) are the side lengths of the triangle and \(\displaystyle A\) is the triangle area.
Or
\(\displaystyle r = \frac{a}{2\sin A}\), where \(\displaystyle a = \overline{PR}\) and \(\displaystyle A\) the angle opposite to it.
The formula gives the radius of the circle for any triangle inscribed inside when all vertices of the triangle touch the circumference of the circle.
If you are not allowed to use this formula and you want to solve the problem using pure geometry, you can construct the perpendicular bisectors.

Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
I corrected his error in #4. Did you not see that? Replace Q with O there.
blamocur
Elite Member
- Joined
- Oct 30, 2021
- Messages
- 3,220
Did not at first notice the red OI think there's a typo there:
In particular, OM = 15 - r.
blamocur
Elite Member
- Joined
- Oct 30, 2021
- Messages
- 3,220
My bad. As @Dr.Peterson noted, it should OM, not QM.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
Since you got a different answer, what you did is simply wrong. The question is, why?
First, this work accomplished nothing:
Then, the following is just wrong; there's a major sign error:
In fact, [imath]r^2-(15-r)^2=r^2-(225-30r+r^2)=30r-225[/imath]. So the next line should be
First, this work accomplished nothing:
Then, the following is just wrong; there's a major sign error:
In fact, [imath]r^2-(15-r)^2=r^2-(225-30r+r^2)=30r-225[/imath]. So the next line should be
[imath]30r-225=64\\30r=289\\r=289/30\approx9.63[/imath]
blamocur
Elite Member
- Joined
- Oct 30, 2021
- Messages
- 3,220