angle formed by two lines in Space

P

Perlita

New member
Joined
Oct 4, 2013
Messages
9
Hello,
I'm confused about this question... Given the cube below, we draw two diagonals AM and MC as shown.
What's the measure of the angle formed by these two diagonals?

pb26.jpg
I know it's not 90 degrees, as we're working in two different planes, but can't figure out what to do...
 
Perlita said:
Hello,
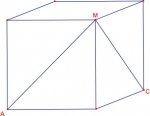
I'm confused about this question... Given the cube below, we draw two diagonals AM and MC as shown.
What's the measure of the angle formed by these two diagonals?

View attachment 4054
I know it's not 90 degrees, as we're working in two different planes, but can't figure out what to do...
Click to expand...

Think about. The diagonal AC has the same length as AM & MC. So what \(\displaystyle \Delta AMC~?\)
 
You know, I presume, that all faces of a cube are identical so that, in particular, all diagonals of those faces have the same length? If you draw a third diagonal, AC, you will have a triangle, all of whose sides have the same length. What is such a triangle called? What is true about the angles of such a triangle?
 
In this case, the triangle is equilateral and the angle measures 60 degrees.
Is this the final answer?
 
You must log in or register to reply here.
Top