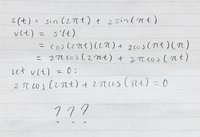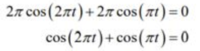Please refer to the attachments:
I do not really understand this question, and I am stuck on how to do it. What does "in the first cycle of its motion" mean? From 0 to 2pi because it is sine???
When I attempted this question, I understood that you would need to differentiate the displacement function to get the velocity function, where you would then set the velocity function equal to 0 because that is when the particle would be stationary (refer to attachment B). However, looking at the worked solution, I do not understand the simplification of the velocity function that they do (refer to red arrow with question mark in attachment). I also do not understand what they do from then onwards...
Thank you!
I do not really understand this question, and I am stuck on how to do it. What does "in the first cycle of its motion" mean? From 0 to 2pi because it is sine???
When I attempted this question, I understood that you would need to differentiate the displacement function to get the velocity function, where you would then set the velocity function equal to 0 because that is when the particle would be stationary (refer to attachment B). However, looking at the worked solution, I do not understand the simplification of the velocity function that they do (refer to red arrow with question mark in attachment). I also do not understand what they do from then onwards...
Thank you!