You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
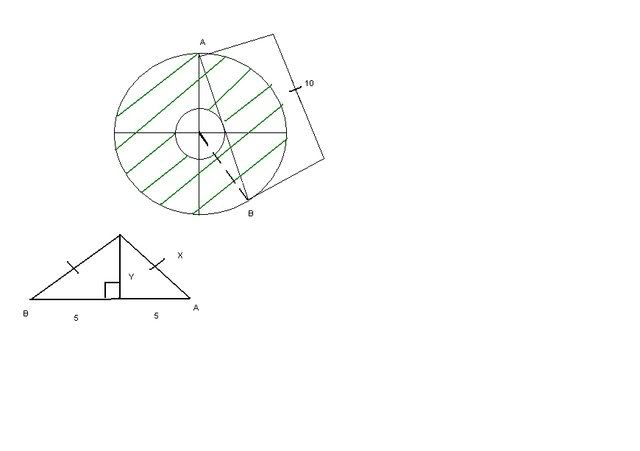
Area of shaded region?
- Thread starter Seb
- Start date
I think you are calling the radius of the big circle x and that of the small circle y.
Shaded area = area of big circle - area of small circle.
Convert that sentence to an equation.
Then realize that using the Pythagorean Theorem you can arrive at x^2 - y^2 = 5^2.
Look at these two equations. Factor out a pi in one of them and see if you can make a substitution that will yield your answer.
Shaded area = area of big circle - area of small circle.
Convert that sentence to an equation.
Then realize that using the Pythagorean Theorem you can arrive at x^2 - y^2 = 5^2.
Look at these two equations. Factor out a pi in one of them and see if you can make a substitution that will yield your answer.
Seb said:Hey, I had needed some help on this problem. It was to Find the area of the shaded region. So far this is all I have gotten. Not sure but it should all be right up till this point.
It would apppear that you area trying to find the difference in area between the large circle and the small circle given the length of a chord tangent to the inner circle.
Let the radius of the inner circle be "r" and that of the outer circle "R". Let` the chord length be "C".
Drawing a line from the circle ecnter to the end of the chord and a line from the center to the point of tangency of the chord to the circle.
This create a triangle with sides equal to C/2 and "r" with hypotenuse of "R".
Then, we are looking for A = PiR^2 - Pir^2.
R^2 = r^2 + (C/2)^2
Substituting, A = Pi(r^2 + (C/2)^2) - Pir^2
Expanding, A = Pir^2 + Pi(C/2)^2- Pir^2 = (PiC)/2.