math_Lover
New member
- Joined
- Dec 8, 2020
- Messages
- 5
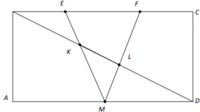
In the rectangle ABCD the side BC is divided into three equal parts by points E and F (see the figure): |BE| = |EF| = |FC|.
The point M divides the side AD into two equal parts (|AM| = |MD|).
The diagonal BD intersects straight lines EM and FM in points K and L respectively.
Find the area of the triangle MKL if the area of the rectangle ABCD equals 280.
The point M divides the side AD into two equal parts (|AM| = |MD|).
The diagonal BD intersects straight lines EM and FM in points K and L respectively.
Find the area of the triangle MKL if the area of the rectangle ABCD equals 280.

