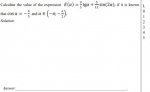Christofor
New member
- Joined
- Jul 28, 2018
- Messages
- 2
Calculate value of E(a)=(4/5)tg(a)+(5/12)sin(2a), if cos(a) = -4/5, a ∈ (-pi; -pi/2)
Hi, I am a student and I do exercises at home from past exams to get ready for the test for next summer and I have a problem that I can't finish it.
Calculate the value of the expression E(a)=(4/5)tg(a)+(5/12)sin(2a), if it is known that cos(a) and a ∈ (-pi; -pi/2). (see the photo)
What I did: (4/5)tg(a)+(5/12)sin(2a) = (4/5)tg(a)+(5/12)*2sin(a)cos(a)
(4/5)tg(a)+(5/6)sin(a)cos(a) = (4/5)tg(a)+(5/6)sin(a)*(-4/5)
4/5(tg(a)-(5/6)sin(a)) and here I stuck.
Here are given points for: 1p for obtaining sin(a)^2 = 9/25 ( here is sin(a)*sin(a) not sin(a^2) )
1p for obtaining sin(a) = -3/5
1p for obtaining sin(2a) = 24/25
1p for obtaining tg(a) =3/4
1p for obtaining E(a) =1
Can someone help me, please?
Hi, I am a student and I do exercises at home from past exams to get ready for the test for next summer and I have a problem that I can't finish it.
Calculate the value of the expression E(a)=(4/5)tg(a)+(5/12)sin(2a), if it is known that cos(a) and a ∈ (-pi; -pi/2). (see the photo)
What I did: (4/5)tg(a)+(5/12)sin(2a) = (4/5)tg(a)+(5/12)*2sin(a)cos(a)
(4/5)tg(a)+(5/6)sin(a)cos(a) = (4/5)tg(a)+(5/6)sin(a)*(-4/5)
4/5(tg(a)-(5/6)sin(a)) and here I stuck.
Here are given points for: 1p for obtaining sin(a)^2 = 9/25 ( here is sin(a)*sin(a) not sin(a^2) )
1p for obtaining sin(a) = -3/5
1p for obtaining sin(2a) = 24/25
1p for obtaining tg(a) =3/4
1p for obtaining E(a) =1
Can someone help me, please?