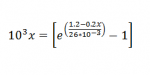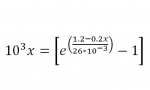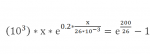can you help me with it: (10^3)x = e^[(1.2-0.2x)/(26*10^(-3))] - 1

[im alex]

Can you help me with it

\(\displaystyle \Large{10^3\, x\, =\, \left[\, e^{\left(\frac{1.2-0.2x}{26\cdot10^{-3}}\right)}\, -\, 1\right]}\)

 

[Deleted member 4993]

\(\displaystyle \Large{10^3\, x\, =\, \left[\, e^{\left(\frac{1.2-0.2x}{26\cdot10^{-3}}\right)}\, -\, 1\right]}\)

With what? What is your question?

You have not replied to any of the helps that tutors posted previously to your other queries!!

 

[im alex]

With what? What is your question?

You have not replied to any of the helps that tutors posted previously to your other queries!!

well I'm purely sorry khan my access to the internet was quit hard back then but I hop you guys accept my apology

 

[Deleted member 4993]

\(\displaystyle \Large{10^3\, x\, =\, \left[\, e^{\left(\frac{1.2-0.2x}{26\cdot10^{-3}}\right)}\, -\, 1\right]}\)

What is being asked in this problem?

What do you need to do?

What are your thoughts?

Please share your work with us ...even if you know it is wrong.

If you are stuck at the beginning tell us and we'll start with the definitions.

You need to read the rules of this forum. Please read the post titled "Read before Posting" at the following URL:

http://www.freemathhelp.com/forum/announcement.php?f=33

 

[im alex]

I went through to organize it until but i don't know what to do after that

 

[stapel]

I went through to organize it until

\(\displaystyle \large{\left(10^3\right)\, \cdot\, x\, \cdot\, e^{0.2\cdot\frac{x}{26\cdot 10^{-3}}}\, =\, e^{\frac{200}{26}}\, -\, 1}\)

but i don't know what to do after that

We still don't know what to do with this, either, because you still haven't provided any instructions. In fact, though you've posted this to "Differential Equations", it doesn't appear to be that sort of an equation.

Please reply with the multiply-requested information; namely, the instructions for this equation. When you reply, please show the steps by which you arrived at your new equation above. Thank you!

 

[HallsofIvy]

That appears to be the "transcendental equation" Axe^(Bx)= C where A, B, and C are the constants (I will let you do the arithmetic). That does not have an "algebraic" solution but can be solved using Lambert's "W" function which is defined as the inverse function to f(x)= xe^x. If we let u= Bx then x=u/B and the equation can be written A(u/B)e^u= C or ue^u= BC/A. Then u= W(BC/A) so that x= W(BC/A)/B.