escribblings
New member
- Joined
- Jan 25, 2015
- Messages
- 8
Hi. First post so go gentle.
Just for background I got a Grade C GCSE in Statistics (and RSA Stage 1 (I think) at the same time) in 1994 and a Grade B GCSE in Mathematics in 1995. So I'm not a complete dunce, but I am very rusty.
What I am trying to work out here is not for any course work, it is for a personal project. Many people would probably have accepted a rough answer by now, but I like challenges - and now this one has bested me and I am desperately trying to figure it out.
So here it is.
I am trying to calculate the viewing angle required of a CCTV camera to view a set area at a set distance. More specifically, to be able to view said area in sufficient detail to make out personal features. In doing research, I have come across a statement that says the the minimum requirement for facial recognition is 40 pixels per foot. As such, a camera with a VGA resolution of 640p×480p would in theory be able to pick out a face over an area of 16'×12'.
If I were to mount the camera directly opposite and central to the area I wish to view, I would have no issues calculating the viewing angle of the camera.
e.g.
The camera is mounted 60' from the area to be viewed which is 16'×12'.
Now there is still one aspect I am unsure of, and that is how the cameras viewing angle is measured, but that is a minor detail and once I know the correct way I can factor that in accordingly. In the mean time I will solve the viewing angle for the above situation using both methods. In both methods we know that camera is perfectly central to the viewing area.
Method 1: Viewing angle based on the width of the area.
In this instance we are looking at a tetrahedron with a base of 16'×12' and a height of 60'. As those are the only measurements we currently have the easiest option is to split it down the centre and use Pythagoras on the remaining half.
Method 2: Viewing angle based on the diagonal of the area.
This is much the same as method 1, but this time we are looking at a cone with a base diameter of 20' (the diagonal of the area) and a height of 60' (but flattened into a triangle for this problem)
Method 1:
√((16÷2)²+60²) = 60.539'
Method 2: Is practically the same, but requires solving the hypotenuse of the viewing area.
√(16²+12²) = 20
√((20÷2)²+60²) = 60.828'
2 slightly different answers, but as I say I can factor in the correct one later.
The issue I have is that both of the above equations simply assume the top point of the cone or tetrahedron is perfectly central to the base.
However, the camera will be mounted 20' above ground level, and at least 10' to the side of the area to be viewed. And this is where I am falling down. Because i want to still be able to view the entire vertical area of 16'×12' at 40px/ft, even though the plane is not perpendicular to the point of origin, if that makes sense.
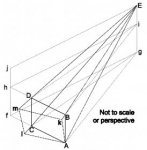
If this helps, here are the X,Y,Z co-ordinates of the 4 corners for the area to be viewed.
A - 0,0,0
B - 0,0,16
C - 0,12,0
D - 0,12,16
and the co-ordinates for the position of the camera
Starting position
E - 60,6,8
New position
F - 60,20,26
The plane of 16'×12' will somehow slice across the base of the tetrahedron or cone, which will rotate about point D until point E is in line with and extended to point F. And then the angle widened to make sure all other points are included.
Can anyone help?
[Edit]
It struck me overnight that I may not be successful in getting the entire area I want to view at the correct definition level.
In this case the top left corner (C 0,12,0) is more important than the bottom right (B 0,0,16).
But I would also be interested to know what the minimum resolution needed would be to get the 16'×12' area at that distance, height and offset.
P.s. I am quite happy to do the math, I'm am just not sure how to go about it.
[/edit]
Just for background I got a Grade C GCSE in Statistics (and RSA Stage 1 (I think) at the same time) in 1994 and a Grade B GCSE in Mathematics in 1995. So I'm not a complete dunce, but I am very rusty.
What I am trying to work out here is not for any course work, it is for a personal project. Many people would probably have accepted a rough answer by now, but I like challenges - and now this one has bested me and I am desperately trying to figure it out.
So here it is.
I am trying to calculate the viewing angle required of a CCTV camera to view a set area at a set distance. More specifically, to be able to view said area in sufficient detail to make out personal features. In doing research, I have come across a statement that says the the minimum requirement for facial recognition is 40 pixels per foot. As such, a camera with a VGA resolution of 640p×480p would in theory be able to pick out a face over an area of 16'×12'.
If I were to mount the camera directly opposite and central to the area I wish to view, I would have no issues calculating the viewing angle of the camera.
e.g.
The camera is mounted 60' from the area to be viewed which is 16'×12'.
Now there is still one aspect I am unsure of, and that is how the cameras viewing angle is measured, but that is a minor detail and once I know the correct way I can factor that in accordingly. In the mean time I will solve the viewing angle for the above situation using both methods. In both methods we know that camera is perfectly central to the viewing area.
Method 1: Viewing angle based on the width of the area.
In this instance we are looking at a tetrahedron with a base of 16'×12' and a height of 60'. As those are the only measurements we currently have the easiest option is to split it down the centre and use Pythagoras on the remaining half.
Method 2: Viewing angle based on the diagonal of the area.
This is much the same as method 1, but this time we are looking at a cone with a base diameter of 20' (the diagonal of the area) and a height of 60' (but flattened into a triangle for this problem)
Method 1:
√((16÷2)²+60²) = 60.539'
Method 2: Is practically the same, but requires solving the hypotenuse of the viewing area.
√(16²+12²) = 20
√((20÷2)²+60²) = 60.828'
2 slightly different answers, but as I say I can factor in the correct one later.
The issue I have is that both of the above equations simply assume the top point of the cone or tetrahedron is perfectly central to the base.
However, the camera will be mounted 20' above ground level, and at least 10' to the side of the area to be viewed. And this is where I am falling down. Because i want to still be able to view the entire vertical area of 16'×12' at 40px/ft, even though the plane is not perpendicular to the point of origin, if that makes sense.
If this helps, here are the X,Y,Z co-ordinates of the 4 corners for the area to be viewed.
A - 0,0,0
B - 0,0,16
C - 0,12,0
D - 0,12,16
and the co-ordinates for the position of the camera
Starting position
E - 60,6,8
New position
F - 60,20,26
The plane of 16'×12' will somehow slice across the base of the tetrahedron or cone, which will rotate about point D until point E is in line with and extended to point F. And then the angle widened to make sure all other points are included.
Can anyone help?
[Edit]
It struck me overnight that I may not be successful in getting the entire area I want to view at the correct definition level.
In this case the top left corner (C 0,12,0) is more important than the bottom right (B 0,0,16).
But I would also be interested to know what the minimum resolution needed would be to get the 16'×12' area at that distance, height and offset.
P.s. I am quite happy to do the math, I'm am just not sure how to go about it.
[/edit]
Last edited: