Challenge

logistic_guy

logistic_guy

Senior Member
Joined
Apr 17, 2024
Messages
2,214
\(\displaystyle \overrightarrow{SQ}\) bisects \(\displaystyle \angle RST\), \(\displaystyle \overrightarrow{SP}\) bisects \(\displaystyle \angle RSQ\), and \(\displaystyle \overrightarrow{SV}\) bisects \(\displaystyle \angle RSP\). The measure of \(\displaystyle \angle VSP\) is \(\displaystyle 17^{\circ}\). Find \(\displaystyle m\angle TSQ\). Explain.
 
Beer drenched reaction follows.
logistic_guy said:
\(\displaystyle \overrightarrow{SQ}\) bisects \(\displaystyle \angle RST\), \(\displaystyle \overrightarrow{SP}\) bisects \(\displaystyle \angle RSQ\), and \(\displaystyle \overrightarrow{SV}\) bisects \(\displaystyle \angle RSP\). The measure of \(\displaystyle \angle VSP\) is \(\displaystyle 17^{\circ}\). Find \(\displaystyle m\angle TSQ\). Explain.
Click to expand...
logistic_guy said:
\(\displaystyle \textcolor{blue}{68^{\circ}}\)


Well, I will leave this part for the audience to think!
Click to expand...
Relax laddie.
This is hardly a challenge and there's very little to think about.

Screenshot_20250804-212038_Chrome.jpg

Maybe you'll enjoy this little challenge that I came across sometime ago.

Screenshot_20250804-204935_Gallery.jpg
 
Last edited:
jonah2.0 said:
This is hardly a challenge and there's very little to think about.
Click to expand...
It is. The difficulty is not how to find the value of the angle after you get the right sketch. It is rather how to sketch the given information correctly. And thank you for the sketch babie!

jonah2.0 said:
Maybe you'll enjoy this little challenge that I came across sometime ago.
Click to expand...
Sure. I will work on it. But I don't cheat, so it will take me some time! We are able to solve problems related to the collision of two atoms, do you think that this problem is more difficult?

😏😏
 
Last edited:
jonah2.0 said:
Beer drenched non sequitur ramblings follow.

Once you have their money, you never give it back.
Click to expand...
At first glance. I have noticed the following.

\(\displaystyle \Delta ABC \sim \Delta DBE\)

Then,

\(\displaystyle \frac{AB}{DB} = \frac{BC}{BE} = \frac{AC}{DE}\)

I am half way to the glory!

😍🥳🤩
 
Beer drenched reaction follows.
logistic_guy said:
... We are able to solve problems related to the collision of two atoms, ...
Click to expand...
What's this "We"?
Are you referring to just yourself, your ego, your echo, and your shadow?
Or is there more than one person behind logistic_guy's username/account?
It would sure explain a lot on how logistic_guy seems incompetent with rather simple geometry stuff and yet looking like some capable jack of all trades in other posts if it's the latter case.
Just wondering.
 
jonah2.0 said:
What's this "We"?
Click to expand...
We \(\displaystyle \rightarrow\) me, myself, and mario\(\displaystyle 99\).

It could also refer to anyone who understands quantum theory and the models of the atom.

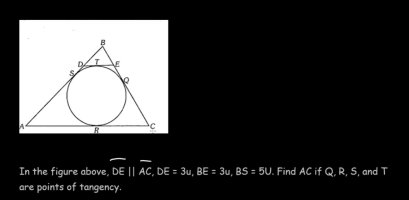
You, Aion, Highlander, professor Dave, and many others have been solving geometry for years. It is true that you all are better than me (for now) in this field as I have just started recently, but I have collected enough Theorems and ideas to push me forward.

Now I am trying to understand how the circle inscribed inside is going to help me solve this problem. I made the point \(\displaystyle O\) as the center of the circle. Now we have this extra information:

\(\displaystyle SO = TO = QO = RO\)

It is better to provide a sketch for future calculations.

jonah_3.png


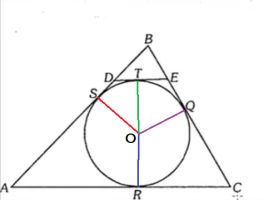
Also we have:

\(\displaystyle AS = AR\)
\(\displaystyle CQ = CR\)
\(\displaystyle BS = BQ\)

jonah2.0 said:
you'll enjoy this little challenge
Click to expand...
You're right, I am enjoying by figuring out little facts about this problems slowly. Because I don't like to cheat I will have to open my geometry book and read more about the properties of circles inscribed inside triangles.
 
Last edited:
I spent a lot of time to come up with the following.

In post number \(\displaystyle 6\), I said:

\(\displaystyle \frac{AB}{DB} = \frac{BC}{BE} = \frac{AC}{DE}\)

For now, I will use:

\(\displaystyle \frac{BC}{BE} = \frac{AC}{DE}\)

Or

\(\displaystyle \frac{BQ + QC}{BE} = \frac{AR + RC}{DE}\)

Or

\(\displaystyle \frac{5 + QC}{3} = \frac{AR + RC}{3}\)

We know that \(\displaystyle QC = RC\), then

\(\displaystyle \frac{5 + RC}{3} = \frac{AR + RC}{3}\)

\(\displaystyle 5 + RC = AR + RC\)

\(\displaystyle AR = 5\)

We know that

\(\displaystyle BQ = BS = 5\)

\(\displaystyle BQ = BE + EQ\)

\(\displaystyle EQ = BQ - BE = 5 - 3 = 2\)

\(\displaystyle ET = EQ = 2\)

\(\displaystyle DT = DE - ET = 3 - 2 = 1\)

\(\displaystyle DS = DT = 1\)

\(\displaystyle BD = BS - DS = 5 - 1 = 4\)

We go back to post # \(\displaystyle 6\)

\(\displaystyle \frac{AB}{DB} = \frac{BC}{BE} = \frac{AC}{DE}\)

I will use now:

\(\displaystyle \frac{AB}{DB} = \frac{AC}{DE}\)

Or

\(\displaystyle \frac{AS + SB}{DB} = \frac{AC}{DE}\)

\(\displaystyle AS = AR = 5\), then

\(\displaystyle \frac{5 + 5}{4} = \frac{AC}{3}\)

\(\displaystyle \frac{10}{4} = \frac{AC}{3}\)

\(\displaystyle \frac{5}{2} = \frac{AC}{3}\)

\(\displaystyle 15 = 2AC\)

Or

\(\displaystyle AC = \frac{15}{2} = \textcolor{blue}{7.5 \ \text{u}}\)
 
You must log in or register to reply here.
Top