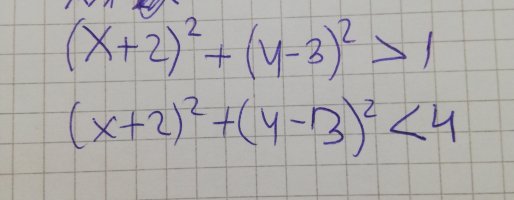Circular ring

L

Loki123

Full Member
Joined
Sep 22, 2021
Messages
790
Apparently since this equation is bigger than 1 and smaller than 4, it makes a circular ring. How?
IMG_20220415_191153.jpg
 
Loki123 said:
the question was:
which locus is this?
Click to expand...
i thought it was a circle because it fits it shape and could easily just equal 3 or 2, or something in between 1 and 4. However, apparently it's a circular ring bc it's bigger than 1 and smaller than 4. I am very confused about it. Circular ring is, if i am not mistaken, two circles, not connected. So how can it be a locus? Or is it wrong that I view locus as one line.
 
Loki123 said:
Apparently since this equation is bigger than 1 and smaller than 4, it makes a circular ring. How?
View attachment 32166
Click to expand...
I was about to post (before I saw the later post about the question asking for the "locus"):-

     As I'm sure you are aware, the equation of a circle may be written as:-

\(\displaystyle (x-a)^2+(y-b)^2=r^2\)​
     where \(\displaystyle (a, b)\) represents the centre of the circle, and \(\displaystyle r^2\) is the radius.

     Therefore, if the values of the the two expressions (>1 & <4) are different they will form      an annulus (your "circular ring"?) or, if both have the same value
     (in the range: 1< that value <4), they will just form a circle.

However, having now seen more of the "question", I would suggest that, perhaps, you are expected to calculate the Area of the annulus (ie: the area between the two curves) when the expressions are set to:

\(\displaystyle (x+2)^2+(y-3)^2=1\)
and
\(\displaystyle (x+2)^2+(y-3)^2=4\) ?
​
I may well be wrong on that, of course, but I'm sure BBB (or other) will confirm or comment further.
 
Last edited:
The Highlander said:
I was about to post (before I saw the later post about the question asking for the "locus"):-

     As I'm sure you are aware, the equation of a circle may be written as:-

\(\displaystyle (x-a)^2+(y-b)^2=r^2\)​
     where \(\displaystyle (a, b)\) represents the centre of the circle, and \(\displaystyle r^2\) is the radius.

     Therefore, if the values of the the two expressions (>1 & <4) are different they will form      an annulus (your "circular ring"?) or, if both have the same value
     (in the range: 1< that value <4), they will just form a circle.

However, having now seen more of the "question", I would suggest that, perhaps, you are expected to calculate the Area of the annulus when the expressions are set to:

\(\displaystyle (x-a)^2+(y-b)^2=1\)
and
\(\displaystyle (x-a)^2+(y-b)^2=4\) ?
​
I may well be wrong on that, of course, but I'm sure BBB (or other) will confirm or comment further.
Click to expand...
thank you. I am not supposed to calculate anything I am just supposed to say what locus it represents.
 
Loki123 said:
thank you. I am not supposed to calculate anything I am just supposed to say what locus it represents.
Click to expand...
I see, in that case I would wait for someone else to comment on my suggestion before submitting it as your 'answer' because I'm not at all certain that it's correct, lol.

Maybe someone else will have a better suggestion. ?
 
You need two concentric circles [imath](x+2)^2+(y-3)^2=1~\&~(x+2)^2+(y-3)^2=4[/imath] SEE HERE
The set of points between the two circles is what you want.
Note that no one of those points is on either circle.
 
pka said:
You need two concentric circles [imath](x+2)^2+(y-3)^2=1~\&~(x+2)^2+(y-3)^2=4[/imath] SEE HERE
The set of points between the two circles is what you want.
Note that no one of those points is on either circle.
Click to expand...
okay got it!
 
You must log in or register to reply here.
Top