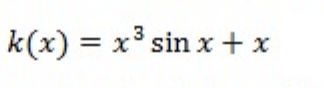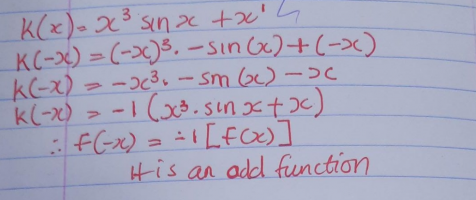Classify the function K(x)=x^3 sinx+x as even or odd
- Thread starter ugu
- Start date
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
1. a*-b is incorrect notation. You need to use parentheses: a*(-b).
2. What is (-a)*(-b)?
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
Check the third line to the fourth line. Arithmetic error.
=
ab
lev888
Elite Member
- Joined
- Jan 16, 2018
- Messages
- 2,995
Correct. But not in your solution.
Steven G
Elite Member
- Joined
- Dec 30, 2014
- Messages
- 14,596
In the third line you have 2 terms, one is positive and one is negative. You can factor all you want, but after factoring, the two terms will still have different signs. Suddenly you got both terms to have the same sign. That means to go and find your error.
No.
For your headline it's to be lower case "k" as in k(x).
That is a trig function, so the given problem should write it as "sin(x)."
When you write it that way, consistently write it that way in your steps.
The instructions are incomplete. They should be: Classify the function
\(\displaystyle k(x) = x^3sin(x) + x \ \ \) as even, odd, or neither.
In your second line, you failed to show every x-variable being substituted
with (-x). Other errors were already mentioned.
Edit \(\displaystyle \ \ \) Here is a possible rewrite without the last step/conclusion:
\(\displaystyle \ \ \ k(x) \ = \ x^3sin(x) \ + \ x \)
\(\displaystyle k(-x) \ = \ (-x)^3sin(-x) \ + \ (-x)\)
\(\displaystyle k(-x) \ = \ [-x^3]*[-sin(x)] \ - \ x\)
\(\displaystyle k(-x) \ = \ \ ?\)
\(\displaystyle k(-x) \ = \ (-x)^3sin(-x) \ + \ (-x)\)
\(\displaystyle k(-x) \ = \ [-x^3]*[-sin(x)] \ - \ x\)
\(\displaystyle k(-x) \ = \ \ ?\)
Now, after simplifying k(-x), how does k(-x) compare to k(x)? Is it equal to
k(x), is it the opposite sign (negation) of k(x), or is it neither of these two?
Last edited:
Thank you sir