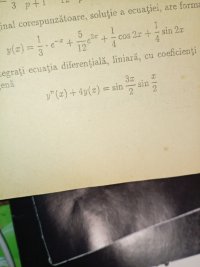Clueless about the Laplace Operational Method

[wolly]

How did my differential equation from that function f(z) changed to this function?
Is there a method?
How did it got y(x)?

 

[logistic_guy]

How does the denominator have these values?

[math]0![/math][math]1![/math][math]2![/math]@logistic_guy
Can you please explain?

The factorial is part of the residue theorem formula.

For example, when the order of pole is \(\displaystyle 1\), you get

\(\displaystyle \frac{1}{(1 - 1)!} = \frac{1}{0!} = \frac{1}{1} = 1\)

when the order of pole is \(\displaystyle 2\), you get

\(\displaystyle \frac{1}{(2 - 1)!} = \frac{1}{1!} = \frac{1}{1} = 1\)

when the order of pole is \(\displaystyle 3\), you get

\(\displaystyle \frac{1}{(3 - 1)!} = \frac{1}{2!} = \frac{1}{2} \)

So z tends to [math]-2i[/math] and [math]2i[/math]?

[math]lim_{z \to 2i} f(z)*(z-2i)*e^{pt}[/math]and
[math]lim_{z \to -2i} f(z)*(z+2i)*e^{pt}[/math]
I mean I don't know how to calculate [math]e^{2it}[/math] and [math]e^{-2it}[/math]!
@logistic_guy

You can use Euler formula to simplify this.

\(\displaystyle e^{2it} = \cos 2t + i\sin 2t\)

Usually when solving, we are interested in the real solution, so we take only \(\displaystyle \cos 2t\)

Also can the result of the limit of the residue have values like i,2i and so on?

Yes it can.

It says in my book that [math]m_k[/math] is the order of multiplicity!

Multiplicity means the order of the pole.

How did my differential equation from that function f(z) changed to this function?
Is there a method?
How did it got y(x)?

Where is \(\displaystyle f(z)\), I cannot see it. The method is usually Laplace transform.

 

[wolly]

Where is \(\displaystyle f(z)\), I cannot see it. The method is usually Laplace transform.

[math]f(z) = \frac{10}{(z^2+4)(z^3-2z^2-z+2)} + \frac{z^2-z-4}{z^3-2z^2-z+2}[/math]

 

[logistic_guy]

[math]f(z) = \frac{10}{(z^2+4)(z^3-2z^2-z+2)} + \frac{z^2-z-4}{z^3-2z^2-z+2}[/math]

Do you want to do it with the Residue theorem or partial fraction decomposition?

 

[wolly]

Do you want to do it with the Residue theorem or partial fraction decomposition?

Residue theorem but I don't understand why you add every pole!
Can you explain that?

 

[wolly]

@logistic_guy That's what my book said that you need to add up every residue of each pole.
The question is why?

 

[logistic_guy]

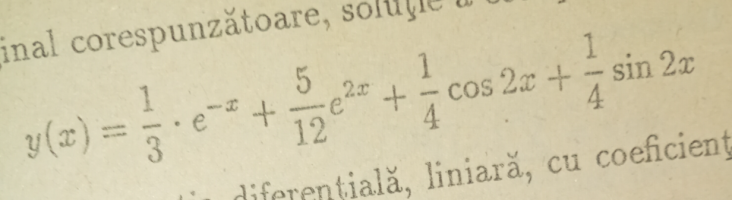
First this solution is only for \(\displaystyle f(z) = \frac{10}{(z^2 + 4)(z^3 - 2z^2 - z + 2)}\). If you add \(\displaystyle f(z) = \frac{z^2 - z - 4}{z^3 - 2z^2 - z + 2}\), you will get a different answer.

Residue theorem but I don't understand why you add every pole!
Can you explain that?

You add them because the solution is usually is done by partial fraction decomposition. Like this

\(\displaystyle f(z) = \frac{10}{(z^2 + 4)(z^3 - 2z^2 - z + 2)} = \frac{A}{z + 2i} + \frac{B}{z - 2i} + \frac{C}{z + 1} + \frac{E}{z - 1} + \frac{F}{z - 2}\)

You find the values of the letters and then you look at the Laplace transform table to get the solution which is mix of sin, cos, and e.

But when you do it with the residue theorem, the formula gives you the answer directly for each term. Then you have to add them to get the full solution.

 

[wolly]

View attachment 39351

First this solution is only for \(\displaystyle f(z) = \frac{10}{(z^2 + 4)(z^3 - 2z^2 - z + 2)}\). If you add \(\displaystyle f(z) = \frac{z^2 - z - 4}{z^3 - 2z^2 - z + 2}\), you will get a different answer.

So if you add these 2 fractions of f(z) you don't get that answer?
So that means that f(z) is only the first fraction and not the second fraction as the answer?

 

[wolly]

@logistic_guy I'm confused!

 

[logistic_guy]

So if you add these 2 fractions of f(z) you don't get that answer?
So that means that f(z) is only the first fraction and not the second fraction as the answer?

Yes it is only the first fraction. And also they forgot to include the term for the pole \(\displaystyle z = 1\) which is \(\displaystyle -e^x\)

@logistic_guy I'm confused!

Yeah, it's normal to be confused. It is a little bit complicated topic. You will need some time to grasp it all. We all were confused too when we first studied it.