CNC task. Is it possible to find length with this data?

[gor]

Hello.
I hope it's correct category, sorry if it's not.

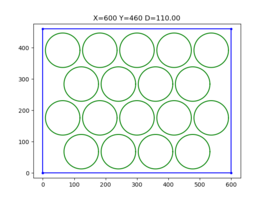
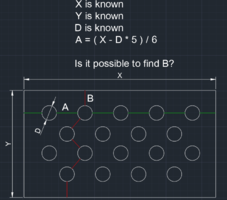
Task for CNC machine to make parametric program, so with different panel sizes holes will follow same pattern.
Some simple trigonometry functions are allowed, like sin, cos but if possible it is better to avoid angles (altho not required).

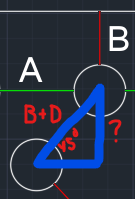
Red lines are equal to each other.
Green lines are equal to each other.

Thanks in advance!

 

[Dr.Peterson]

Task for CNC machine to make parametric program, so with different panel sizes holes will follow same pattern.
Some simple trigonometry functions are allowed, like sin, cos but if possible it is better to avoid angles (altho not required).

Red lines are equal to each other.
Green lines are equal to each other.
View attachment 36443
Thanks in advance!

Here's a little hint, assuming that the holes are meant to be forming squares at a 45 degree angle:

​

What is the length of (?), in terms of B and D?

Then Y = 2B + D + 3*that. You can solve for B.

 

[gor]

Read carefully, panel size can be changed, it's very rare case for a square to be there.

 

[blamocur]

No trigonometry but you can blame Pythogoras for square roots . Let [imath]s[/imath] be the distance between the horizontal rows.
[math]s^2 + \frac{1}{4} (A+D)^2 = (B+D)^2[/math][math]2B + 3s = Y[/math][math]s = \frac{1}{2}\sqrt{4(B+D)^2 - (A+D)^2}[/math][math]B = \frac{Y-3s}{2}[/math]

 

[blamocur]

I hate to admit that my previous post was both incomplete and incorrect . Upon crawling out of the corner I came up with the solution below.
While still using [imath]s[/imath] for the distance between the horizontal rows, we also introduce a couple of variables to keep the expressions from getting too hairy:
[math]f = \frac{A+D}{2} = \frac{X+D}{12}[/math][math]g = Y-D[/math]We can write two equations with uknowns [imath]s[/imath] and [imath]B[/imath]:
[math]s^2 + f^2 = (B+D)^2[/math][math]2B + 3s = Y - D = g[/math]Now we can eliminate [imath]s[/imath] and end up with a single quadratic equation for [imath]B[/imath]:
[math]s = \frac{g-2B}{3}[/math][math]s^2 = (B+D)^2 - f^2 = \frac{1}{9}(g-2B)^2[/math][math]B^2 + 2BD + D^2 - f^2 = \frac{4}{9}B^2 - \frac{4}{9}gB + \frac{1}{9} g^2[/math][math]\frac{5}{9} B^2 + \left(2D + \frac{4}{9}g \right) B + \left(D^2 - f^2 - \frac{1}{9} g^2 \right) = 0[/math]Time to find [imath]B[/imath] from the above quadratic equation:
[math]B = \frac{-Q + \sqrt{Q^2-4PR}}{2P}[/math]where
[math]P = \frac{5}{9}[/math][math]Q = 2D + \frac{4g}{9}[/math][math]R = D^2-f^2-\frac{1}{9}g^2[/math]
To verify those formulae I wrote a quick-and-dirty script, which generated pictures like the one below:

 

[gor]

Spoiler

I hate to admit that my previous post was both incomplete and incorrect . Upon crawling out of the corner I came up with the solution below.
While still using [imath]s[/imath] for the distance between the horizontal rows, we also introduce a couple of variables to keep the expressions from getting too hairy:
[math]f = \frac{A+D}{2} = \frac{X+D}{12}[/math][math]g = Y-D[/math]We can write two equations with uknowns [imath]s[/imath] and [imath]B[/imath]:
[math]s^2 + f^2 = (B+D)^2[/math][math]2B + 3s = Y - D = g[/math]Now we can eliminate [imath]s[/imath] and end up with a single quadratic equation for [imath]B[/imath]:
[math]s = \frac{g-2B}{3}[/math][math]s^2 = (B+D)^2 - f^2 = \frac{1}{9}(g-2B)^2[/math][math]B^2 + 2BD + D^2 - f^2 = \frac{4}{9}B^2 - \frac{4}{9}gB + \frac{1}{9} g^2[/math][math]\frac{5}{9} B^2 + \left(2D + \frac{4}{9}g \right) B + \left(D^2 - f^2 - \frac{1}{9} g^2 \right) = 0[/math]Time to find [imath]B[/imath] from the above quadratic equation:
[math]B = \frac{-Q + \sqrt{Q^2-4PR}}{2P}[/math]where
[math]P = \frac{5}{9}[/math][math]Q = 2D + \frac{4g}{9}[/math][math]R = D^2-f^2-\frac{1}{9}g^2[/math]
To verify those formulae I wrote a quick-and-dirty script, which generated pictures like the one below:
View attachment 36469

I forgot about this thread and opened it by accident ?
Would be unforgivable if so much work was just wasted, ty.
I'll not check it since originally it's not my question but I shared it to a person who asked the question, if he'll see it I'll report back or maybe he will do it
Ty one more time.

(power of internet is amazing)